Data Encryption Standard
In this article, I will show you detail of DES, and of course then implement in Python. As we can heard somewhere that Don't roll your own crypto. But I think in it should be “Don't roll your own crypto and deploy in to production” . From this blogs, I will try implement all cryptography algorithms from scratch, as very naive way, then throw it way!!! Yes, how to learn a cryptography algorithm better then try implement in from scratch, at very begging.
Let’s start with DES, since DES is now considered highly insecure and don’t to use in new system. But lets jump in to detail of DES to see how a modern cryptography algorithm look like to compare with Caesar cipher.
Introduction to Data Encryption Standard (DES)
DES is a symmetric block cipher. The symmetric is, they use a single cryptographic key used for both encrypting and decrypting data. And block cipher mean they encrypt and decrypt a block of data, in case of DES is a block of 64 bits. To compare with stream cipher, only encrypt and decrypt 1 bit on time.
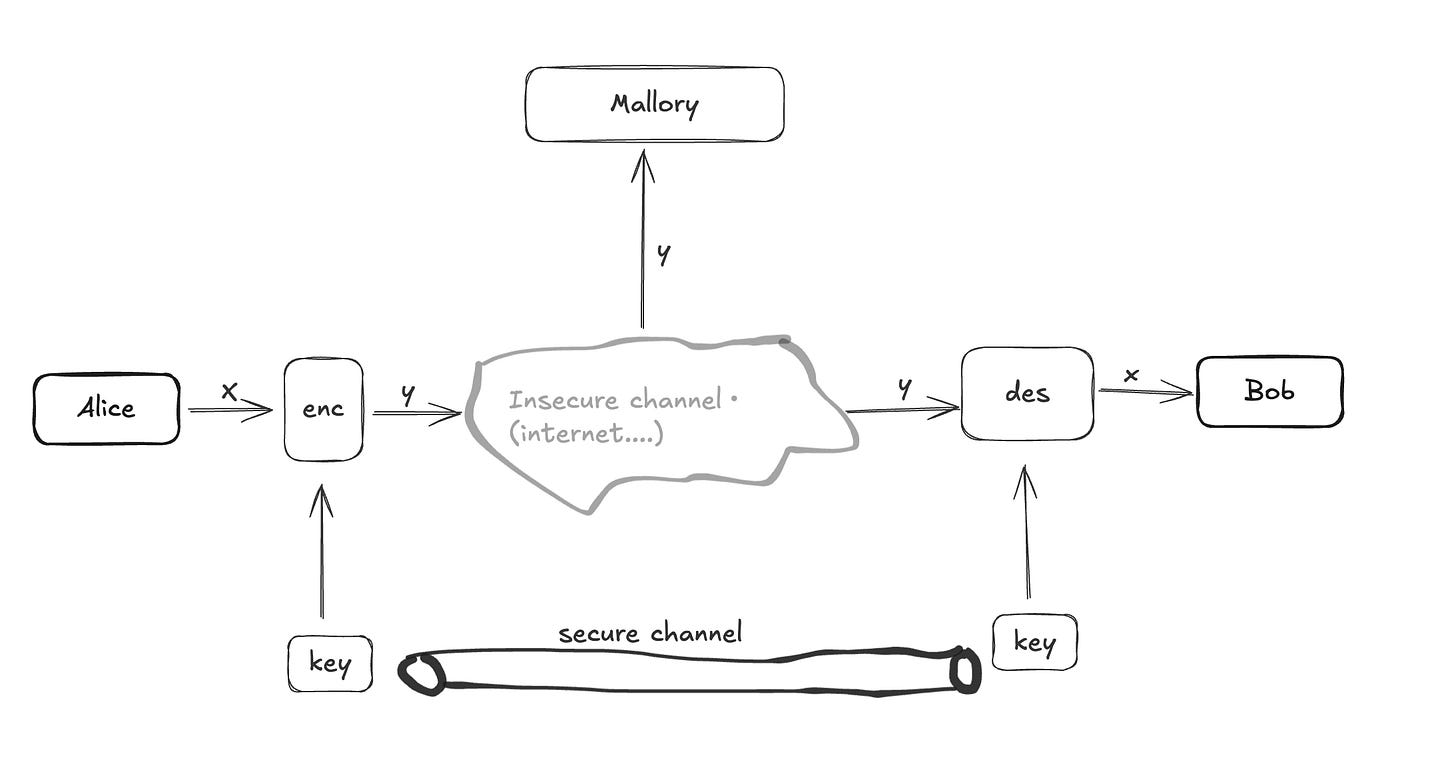
In this scenario, Alice wants to send a message x to Bob over an insecure channel, such as the Internet, and she wants to ensure that Mallory cannot read it. To protect her message, she encrypts it using a function enc() and a key k before sending it.
Later, when Bob get the message, he can decrypt by a function and same key k.
Notes, we call
x is plain text
y is cipher text
k is key
For Malloy, she can get the message y but can’t read, because she don’t know the key. For her they appears as a random sequence of bits. Before encrypting and decrypting, Alice and Bob need to establish a secure channel to agree on the key k.
DES play a role as encryption and decryption functions in the scenario.
DES internal
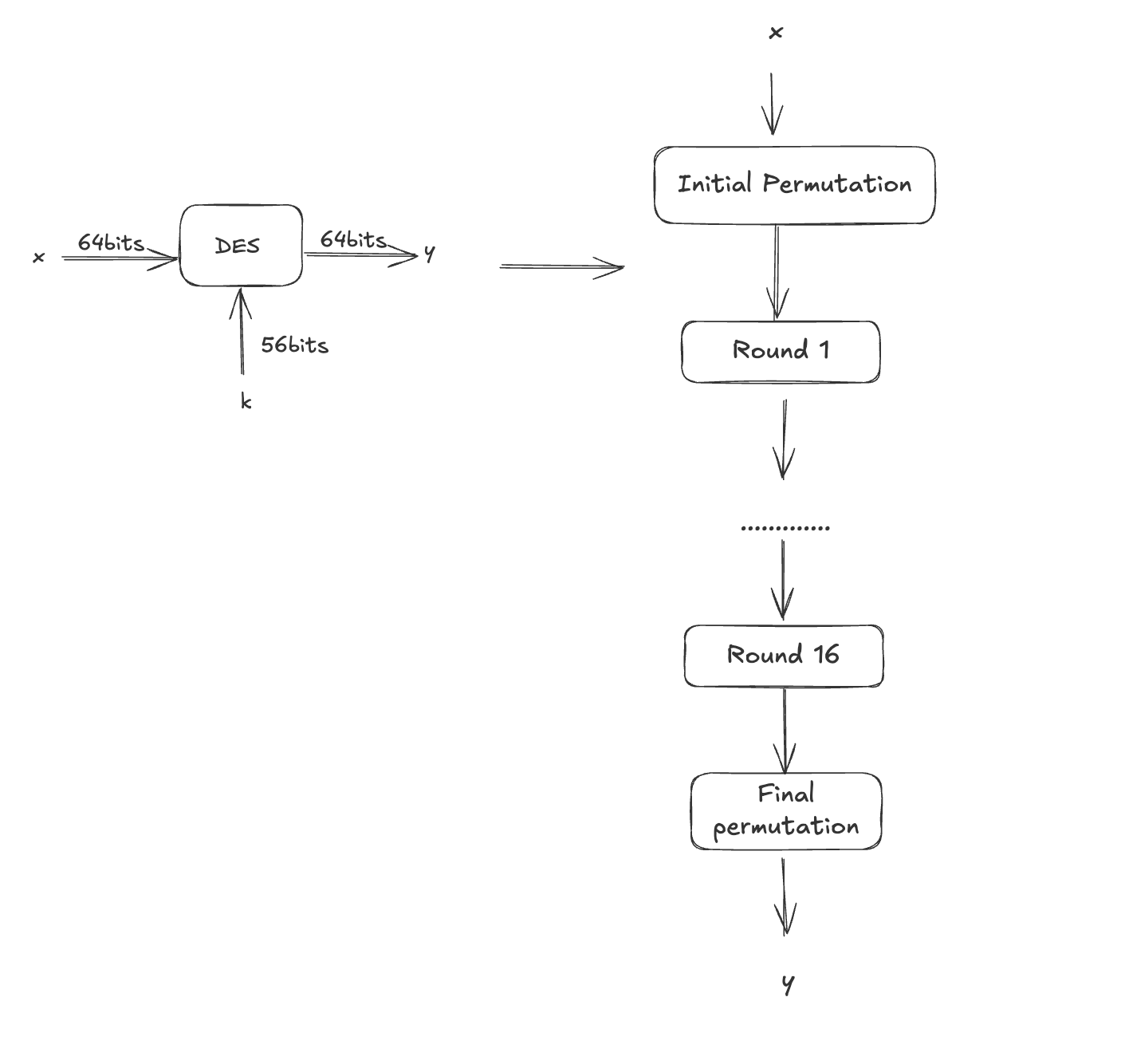
DES takes an input x that is an array 64 bits long, along with a key that is 56 bits long. The output y is also 64 bits in length.
There are two properties of a secure cipher that we need to take into account:
Confusion: Relationship between ciphertext and the encryption key is obscured (hidden, very complex to capture).
Diffusion: if we change a single bit of the plaintext, then about half of the bits in the ciphertext should change
Combine 2 properties in many round can make a secure algorithms.
DES overview
First, the plaintext undergoes an initial permutation (IP), followed by 16 rounds of processing, and concludes with a final permutation (FP).
Let's discuss IP and FP first, and then we'll dive into the details of the 16 rounds.
Initial permutation and final permutation
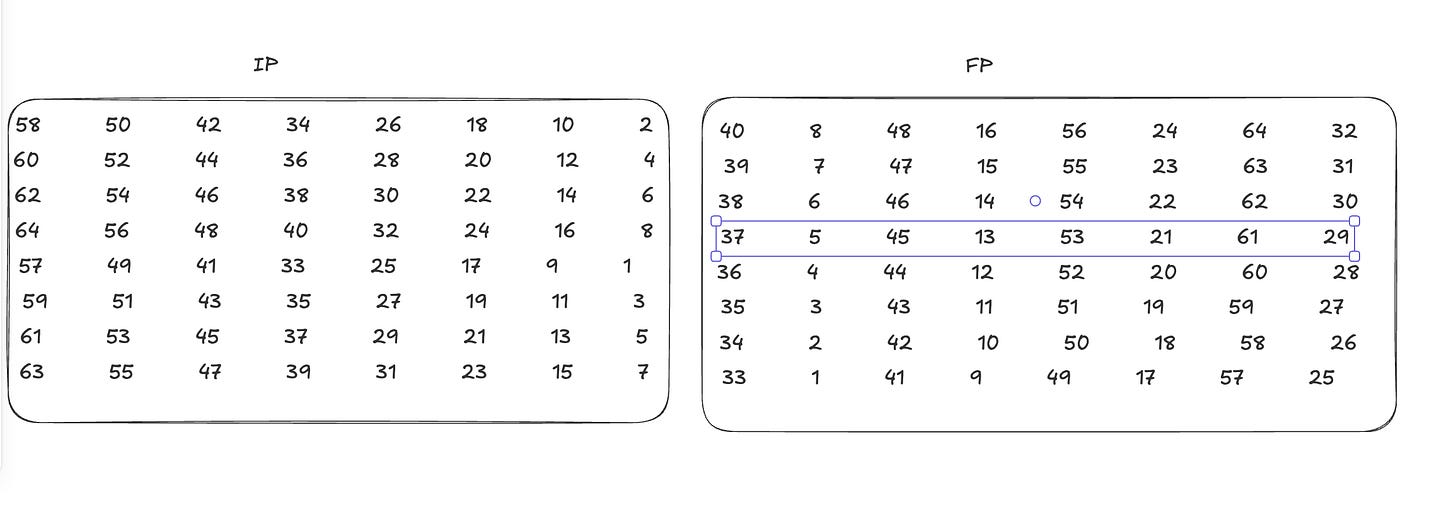
There are 2 tables in DES to show which bit position map to other position. The table IP indicates that input bit 58 is mapped to output position 1, input bit 50 is mapped to the second output position, and so forth. The final permutation FP performs the inverse operation of IP, so the FP table also write as IP−1
Let’s create a function in Python for do it.
| # Initial Permutation (IP) table | |
| IP = [ | |
| 58, 50, 42, 34, 26, 18, 10, 2, | |
| 60, 52, 44, 36, 28, 20, 12, 4, | |
| 62, 54, 46, 38, 30, 22, 14, 6, | |
| 64, 56, 48, 40, 32, 24, 16, 8, | |
| 57, 49, 41, 33, 25, 17, 9, 1, | |
| 59, 51, 43, 35, 27, 19, 11, 3, | |
| 61, 53, 45, 37, 29, 21, 13, 5, | |
| 63, 55, 47, 39, 31, 23, 15, 7 | |
| ] | |
| # Final Permutation (FP) table | |
| FP = [ | |
| 40, 8, 48, 16, 56, 24, 64, 32, | |
| 39, 7, 47, 15, 55, 23, 63, 31, | |
| 38, 6, 46, 14, 54, 22, 62, 30, | |
| 37, 5, 45, 13, 53, 21, 61, 29, | |
| 36, 4, 44, 12, 52, 20, 60, 28, | |
| 35, 3, 43, 11, 51, 19, 59, 27, | |
| 34, 2, 42, 10, 50, 18, 58, 26, | |
| 33, 1, 41, 9, 49, 17, 57, 25 | |
| ] | |
| def permute(block, table): | |
| """ | |
| Permute the block according to the table. | |
| block: 64-bit integer | |
| table: list of 64 integers (1-based positions) | |
| Returns: permuted 64-bit integer | |
| """ | |
| permuted = 0 | |
| for position in table: | |
| bit = (block >> (64 - position)) & 1 | |
| permuted = (permuted << 1) | bit | |
| return permuted | |
| def initial_permutation(block): | |
| """Apply the initial permutation (IP) to a 64-bit block.""" | |
| return permute(block, IP) | |
| def final_permutation(block): | |
| """Apply the final permutation (FP) to a 64-bit block.""" | |
| return permute(block, FP) |
Let’s me explain the function permute in this gist. For easy to understand we will define a small, simplified scenario:
We’ll use an 8-bit block (to visualize easily)
block = 0b11001010(binary for 202)table = [2, 4, 6, 8, 1, 3, 5, 7]
(rearranging the bits: second bit becomes first, fourth becomes second, etc.)
Note: In DES, blocks are 64 bits, but this small version makes the process easier to see.
Position: 1 2 3 4 5 6 7 8
Bits: 1 1 0 0 1 0 1 0 <-- block = 0b11001010
Table: [2, 4, 6, 8, 1, 3, 5, 7]Let’s apply the permutation table [2, 4, 6, 8, 1, 3, 5, 7]. For each new bit position, we pick a bit from the original and replace to new permuted number. Do it manually we can get the result is 10001011.
Let’s go step by step to more understand:
permuted = 0
block = 11001010
table = [2, 4, 6, 8, 1, 3, 5, 7]
Step 1:
- position: 2
- bit = (11001010 << (8 - 2)) & 1
= (11001010 << 6) & 1
= 00000011 & 00000001 = 1
- permuted = (0 << 1) | 1 = 1
Step 2:
- position: 4
- bit = (11001010 << (8 - 4)) & 1
= (11001010 << 4) & 1
= 00001100 & 00000001 = 0
- permuted = (1 << 1) | 0 = 11 | 0 = 10
.....
Step 8
- position: 7
- bit = (0b11001010 >> 1) & 1 = 0b01100101 & 1 = 1
permuted = (1000101 << 1) | 1 = 10001010 | 1 = 10001011
Finally: permuted = 10001011 = 139The main rounds
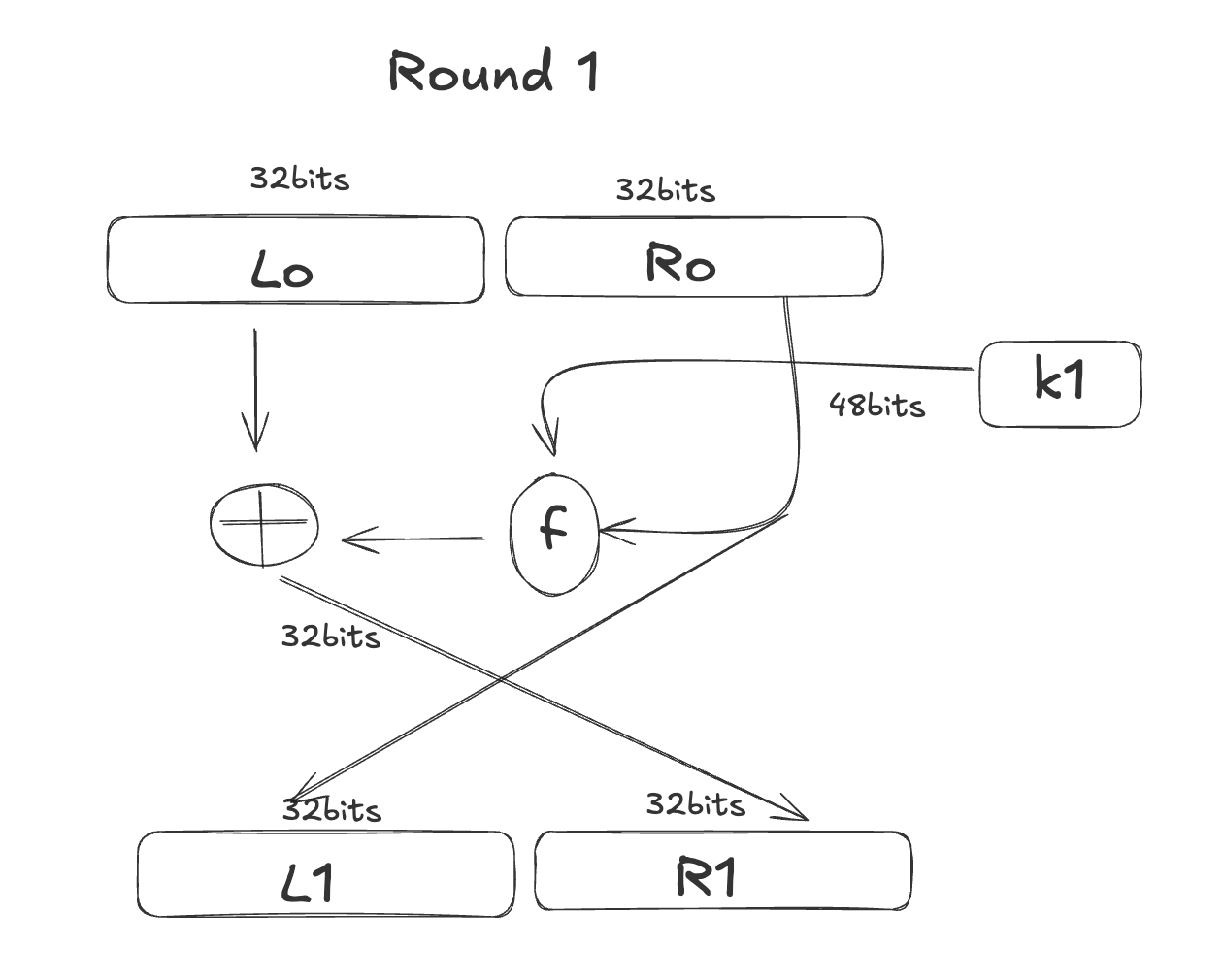
We've completed the two permutation functions, so let's move on to the most important part of DES: the main rounds. There are 16 main rounds in DES, but they all follow the same process, so we only need to analyze one of them.
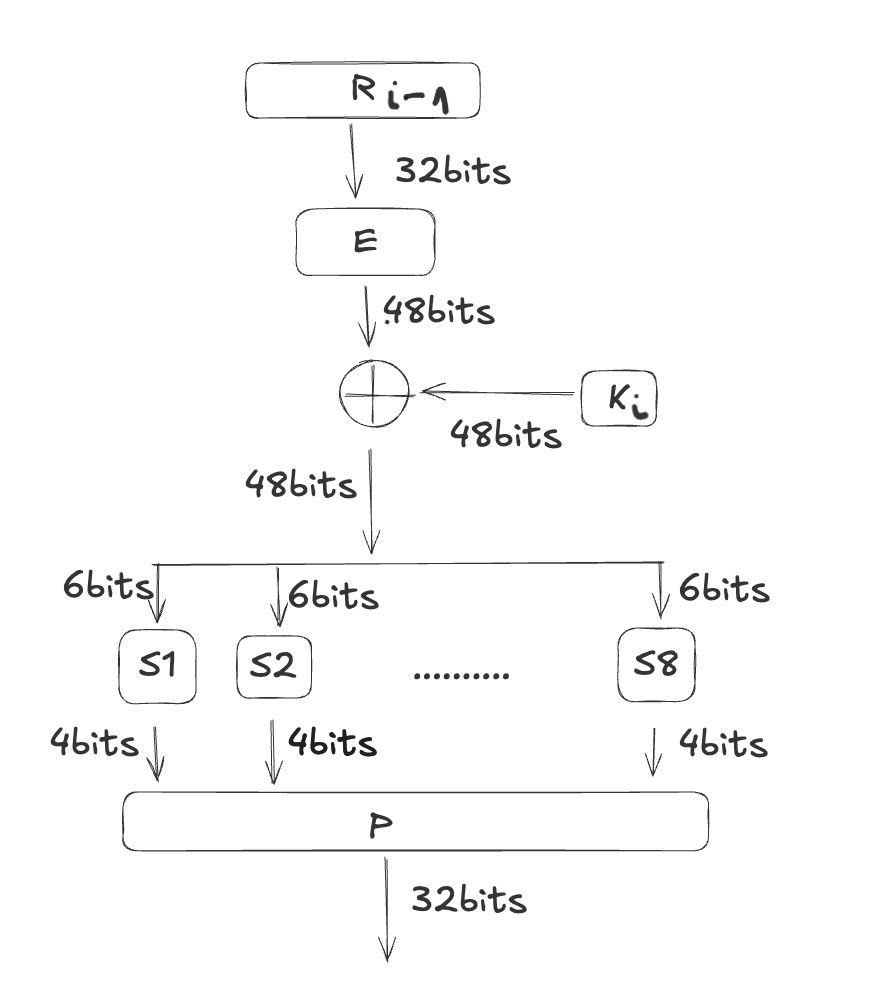
This illustrates Round 1, which is similar for all subsequent rounds. In each round, the output is split into two parts: left and right, with each part consisting of 32 bits. The right part (R) becomes the left part for the next round. Additionally, the right part is input into a function F along with the key, and the output is then XORed with the left part.
As you can see, in DES, each round only encrypt the 1/2 part of data.
The f-function
We now know how each round do, now let’s discuss about detail of the f function. The f-function in DES also call as “The Feistel (F) function”.
Detail of f-function is process 32 bits of data and has 4 steps.
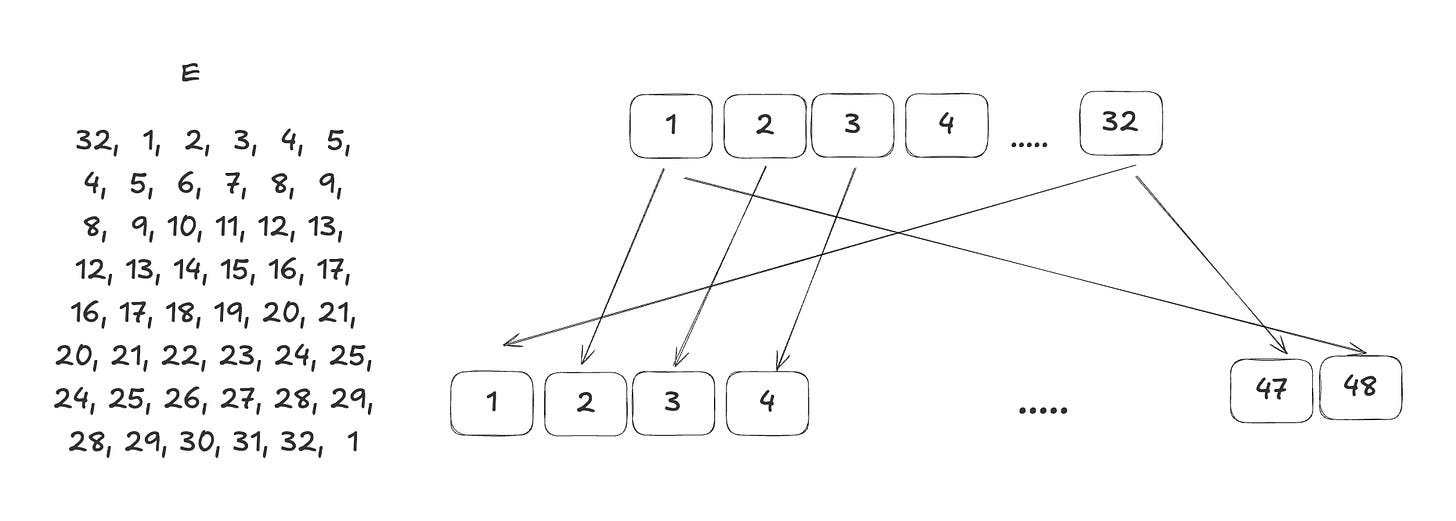
Expansion: The 32-bit half-block is transformed into 48 bits through a process called expansion, marked as E in the diagram. In this process, the 32-bit input is divided into eight 4-bit blocks, and each block is expanded to 6 bits. According to the table E below, 16 of the 32 input bits are duplicated in the output. So the output len is 32 + 16 (duplicated) = 48 bits. For instance, bit number 32 will be replicated as bit number 1 and bit number 47 in the output, while bit number 2 will only be copied once to bit number 3 in the output.
Let’s try to implements those in Python.
| def permute(block, table, in_size): | |
| """Generic permutation function for any size input.""" | |
| permuted = 0 | |
| for position in table: | |
| bit = (block >> (in_size - position)) & 1 | |
| permuted = (permuted << 1) | bit | |
| return permuted | |
| def expansion_function(R): | |
| """ | |
| Expands a 32-bit block R into a 48-bit block using the DES expansion table. | |
| R: 32-bit integer | |
| Returns: 48-bit integer | |
| """ | |
| E_TABLE = [ | |
| 32, 1, 2, 3, 4, 5, | |
| 4, 5, 6, 7, 8, 9, | |
| 8, 9,10,11,12,13, | |
| 12,13,14,15,16,17, | |
| 16,17,18,19,20,21, | |
| 20,21,22,23,24,25, | |
| 24,25,26,27,28,29, | |
| 28,29,30,31,32, 1 | |
| ] | |
| return permute(R, E_TABLE, 32) |
In line 65-71, I just call “permute” function with the E-Table above.
Key Mixing: The new 48 bits are combined with a subkey using an XOR operation. Sixteen 48-bit subkeys—one for each round—are created from the main key using a key schedule. The Python implement by just call “^” each element in expansion output and subkey
\(\begin{aligned} X_i = E(R_{i-1}) \oplus K_i \\ \end{aligned} \)This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersdef key_mixing(expanded_R, subkey): """ XOR the expanded 48-bit R with the 48-bit round subkey. Parameters: expanded_R (int): 48-bit integer from Expansion function subkey (int): 48-bit round subkey Returns: int: 48-bit result of XOR """ return expanded_R ^ subkey
Substitution: After mixing in the subkey, the 48-bit output is split into eight groups of 6 bits each and sent to S-boxes. Each S-box takes 6 bits and gives out 4 bits based on a lookup table. Each S-box contains 2^6 = 64 entries, which are typically represented by a table with 16 columns and 4 rows. Each entry is a 4-bit value. Example for S-box 1 here, the input b = (101001) indicates the row 1yyyy1 (fourth row) and the column x0100x (i.e., the fifth column). If the input b is fed into S-box 1, the output is S1(101001) = 4 = 0100.
Detail of Python code, we process by each 6-bit chunk, get the column and row index then get value in pre-define S-BOX.
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersS_BOXES = [ # S1 [ [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7], [ 0, 15, 7, 4, 14, 2, 13, 1,10, 6, 12,11, 9, 5, 3, 8], [ 4, 1, 14, 8, 13, 6, 2,11,15,12, 9, 7, 3,10, 5, 0], [15,12, 8, 2, 4, 9, 1, 7, 5,11, 3,14,10, 0, 6,13] ], # S2 [ [15, 1, 8,14, 6,11, 3, 4, 9, 7, 2,13,12, 0, 5,10], [ 3,13, 4, 7,15, 2, 8,14,12, 0, 1,10, 6, 9,11, 5], [ 0,14, 7,11,10, 4,13, 1, 5, 8,12, 6, 9, 3, 2,15], [13, 8,10, 1, 3,15, 4, 2,11, 6, 7,12, 0, 5,14, 9] ], # S3 [ [10, 0, 9,14, 6, 3,15, 5, 1,13,12, 7,11, 4, 2, 8], [13, 7, 0, 9, 3, 4, 6,10, 2, 8, 5,14,12,11,15, 1], [13, 6, 4, 9, 8,15, 3, 0,11, 1, 2,12, 5,10,14, 7], [ 1,10,13, 0, 6, 9, 8, 7, 4,15,14, 3,11, 5, 2,12] ], # S4 [ [ 7,13,14, 3, 0, 6, 9,10, 1, 2, 8, 5,11,12, 4,15], [13, 8,11, 5, 6,15, 0, 3, 4, 7, 2,12, 1,10,14, 9], [10, 6, 9, 0,12,11, 7,13,15, 1, 3,14, 5, 2, 8, 4], [ 3,15, 0, 6,10, 1,13, 8, 9, 4, 5,11,12, 7, 2,14] ], # S5 [ [ 2,12, 4, 1, 7,10,11, 6, 8, 5, 3,15,13, 0,14, 9], [14,11, 2,12, 4, 7,13, 1, 5, 0,15,10, 3, 9, 8, 6], [ 4, 2, 1,11,10,13, 7, 8,15, 9,12, 5, 6, 3, 0,14], [11, 8,12, 7, 1,14, 2,13, 6,15, 0, 9,10, 4, 5, 3] ], # S6 [ [12, 1,10,15, 9, 2, 6, 8, 0,13, 3, 4,14, 7, 5,11], [10,15, 4, 2, 7,12, 9, 5, 6, 1,13,14, 0,11, 3, 8], [ 9,14,15, 5, 2, 8,12, 3, 7, 0, 4,10, 1,13,11, 6], [ 4, 3, 2,12, 9, 5,15,10,11,14, 1, 7, 6, 0, 8,13] ], # S7 [ [ 4,11, 2,14,15, 0, 8,13, 3,12, 9, 7, 5,10, 6, 1], [13, 0,11, 7, 4, 9, 1,10,14, 3, 5,12, 2,15, 8, 6], [ 1, 4,11,13,12, 3, 7,14,10,15, 6, 8, 0, 5, 9, 2], [ 6,11,13, 8, 1, 4,10, 7, 9, 5, 0,15,14, 2, 3,12] ], # S8 [ [13, 2, 8, 4, 6,15,11, 1,10, 9, 3,14, 5, 0,12, 7], [ 1,15,13, 8,10, 3, 7, 4,12, 5, 6,11, 0,14, 9, 2], [ 7,11, 4, 1, 9,12,14, 2, 0, 6,10,13,15, 3, 5, 8], [ 2, 1,14, 7, 4,10, 8,13,15,12, 9, 0, 3, 5, 6,11] ] ] def sbox_substitution(input48): """ Applies DES S-box substitution to a 48-bit input. Splits into 8 blocks of 6 bits, substitutes each using S1–S8. Parameters: input48 (int): 48-bit input after expansion and key mixing. Returns: int: 32-bit output from the 8 S-boxes """ output32 = 0 for i in range(8): # Extract 6-bit chunk six_bits = (input48 >> (42 - 6 * i)) & 0b111111 # Get row (first and last bit), column (middle 4 bits) row = ((six_bits & 0b100000) >> 4) | (six_bits & 0b000001) col = (six_bits >> 1) & 0b1111 # Get S-box value (4 bits) sbox_val = S_BOXES[i][row][col] # Append to output (shift left by 4 then OR) output32 = (output32 << 4) | sbox_val return output32
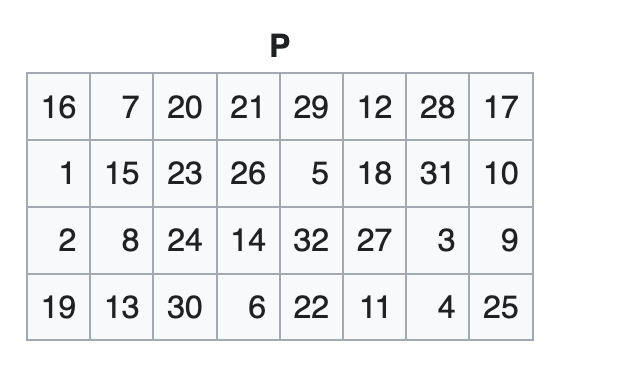
Permutation: Finally, the 32 outputs from the S-boxes are rearranged using a fixed process called the P-box. This ensures that the bits from each S-box in this round are spread out across four different S-boxes in the next round. The Python code is similar with the permutation with a P-Box.
Key Schedule
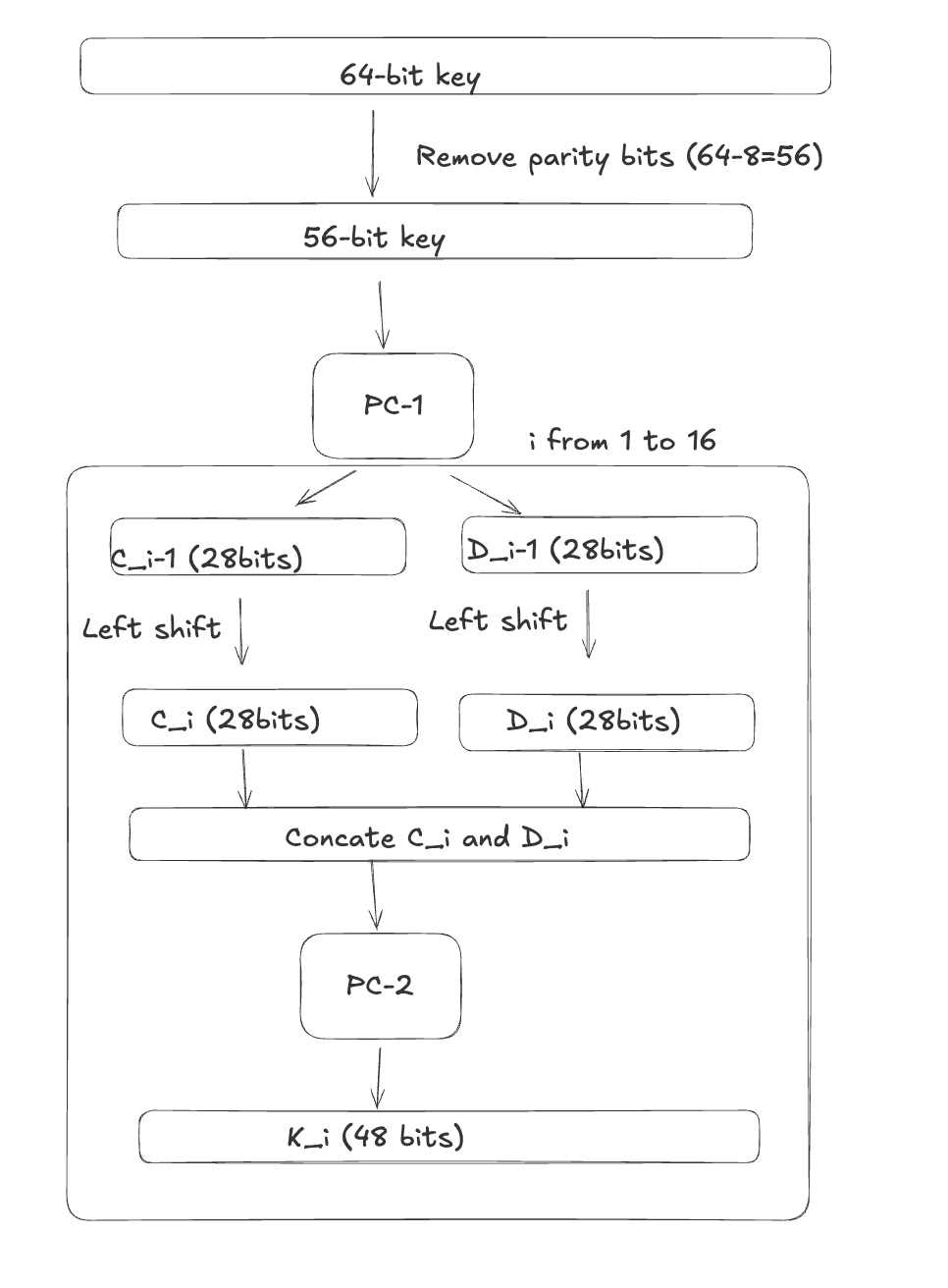
The final steps before we can group together is key schedule. Initially, 56 bits of the key are selected from the initial 64 by Permuted Choice 1 (PC-1)—the remaining eight bits are either discarded or used as parity check bits. The 56 bits are then divided into two 28-bit halves; each half is thereafter treated separately. In successive rounds, both halves are rotated left by one or two bits (specified for each round), and then 48 subkey bits are selected by Permuted Choice 2 (PC-2)—24 bits from the left half, and 24 from the right.
| def left_rotate(val, shift, size): | |
| """Left circular shift""" | |
| return ((val << shift) & ((1 << size) - 1)) | (val >> (size - shift)) | |
| def key_schedule(key64): | |
| """ | |
| Generate 16 DES subkeys (48-bit) from the 64-bit key. | |
| Parameters: | |
| key64 (int): 64-bit integer key | |
| Returns: | |
| List[int]: 16 round keys, each 48 bits | |
| """ | |
| # Tables | |
| PC1 = [ | |
| 57,49,41,33,25,17, 9, | |
| 1,58,50,42,34,26,18, | |
| 10, 2,59,51,43,35,27, | |
| 19,11, 3,60,52,44,36, | |
| 63,55,47,39,31,23,15, | |
| 7,62,54,46,38,30,22, | |
| 14, 6,61,53,45,37,29, | |
| 21,13, 5,28,20,12, 4 | |
| ] | |
| PC2 = [ | |
| 14,17,11,24, 1, 5, | |
| 3,28,15, 6,21,10, | |
| 23,19,12, 4,26, 8, | |
| 16, 7,27,20,13, 2, | |
| 41,52,31,37,47,55, | |
| 30,40,51,45,33,48, | |
| 44,49,39,56,34,53, | |
| 46,42,50,36,29,32 | |
| ] | |
| LEFT_SHIFTS = [1, 1, 2, 2, 2, 2, 2, 2, | |
| 1, 2, 2, 2, 2, 2, 2, 1] | |
| # Step 1: Apply PC-1 | |
| key56 = permute(key64, PC1, 64) | |
| C = (key56 >> 28) & ((1 << 28) - 1) | |
| D = key56 & ((1 << 28) - 1) | |
| round_keys = [] | |
| for shift in LEFT_SHIFTS: | |
| # Step 2: Left shifts | |
| C = left_rotate(C, shift, 28) | |
| D = left_rotate(D, shift, 28) | |
| # Step 3: Combine and apply PC-2 | |
| CD = (C << 28) | D | |
| Ki = permute(CD, PC2, 56) | |
| round_keys.append(Ki) | |
| return round_keys |
Group them together
| IP = [ | |
| 58, 50, 42, 34, 26, 18, 10, 2, | |
| 60, 52, 44, 36, 28, 20, 12, 4, | |
| 62, 54, 46, 38, 30, 22, 14, 6, | |
| 64, 56, 48, 40, 32, 24, 16, 8, | |
| 57, 49, 41, 33, 25, 17, 9, 1, | |
| 59, 51, 43, 35, 27, 19, 11, 3, | |
| 61, 53, 45, 37, 29, 21, 13, 5, | |
| 63, 55, 47, 39, 31, 23, 15, 7 | |
| ] | |
| # Final Permutation (FP) table | |
| FP = [ | |
| 40, 8, 48, 16, 56, 24, 64, 32, | |
| 39, 7, 47, 15, 55, 23, 63, 31, | |
| 38, 6, 46, 14, 54, 22, 62, 30, | |
| 37, 5, 45, 13, 53, 21, 61, 29, | |
| 36, 4, 44, 12, 52, 20, 60, 28, | |
| 35, 3, 43, 11, 51, 19, 59, 27, | |
| 34, 2, 42, 10, 50, 18, 58, 26, | |
| 33, 1, 41, 9, 49, 17, 57, 25 | |
| ] | |
| def permute(block, table, in_size=64): | |
| """Generic permutation function for any size input.""" | |
| permuted = 0 | |
| for position in table: | |
| bit = (block >> (in_size - position)) & 1 | |
| permuted = (permuted << 1) | bit | |
| return permuted | |
| def initial_permutation(block): | |
| """Apply the initial permutation (IP) to a 64-bit block.""" | |
| return permute(block, IP) | |
| def final_permutation(block): | |
| """Apply the final permutation (FP) to a 64-bit block.""" | |
| return permute(block, FP) | |
| def expansion_function(R): | |
| """ | |
| Expands a 32-bit block R into a 48-bit block using the DES expansion table. | |
| R: 32-bit integer | |
| Returns: 48-bit integer | |
| """ | |
| E_TABLE = [ | |
| 32, 1, 2, 3, 4, 5, | |
| 4, 5, 6, 7, 8, 9, | |
| 8, 9,10,11,12,13, | |
| 12,13,14,15,16,17, | |
| 16,17,18,19,20,21, | |
| 20,21,22,23,24,25, | |
| 24,25,26,27,28,29, | |
| 28,29,30,31,32, 1 | |
| ] | |
| return permute(R, E_TABLE, 32) | |
| def key_mixing(expanded_R, subkey): | |
| """ | |
| XOR the expanded 48-bit R with the 48-bit round subkey. | |
| Parameters: | |
| expanded_R (int): 48-bit integer from Expansion function | |
| subkey (int): 48-bit round subkey | |
| Returns: | |
| int: 48-bit result of XOR | |
| """ | |
| return expanded_R ^ subkey | |
| S_BOXES = [ | |
| # S1 | |
| [ | |
| [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7], | |
| [ 0, 15, 7, 4, 14, 2, 13, 1,10, 6, 12,11, 9, 5, 3, 8], | |
| [ 4, 1, 14, 8, 13, 6, 2,11,15,12, 9, 7, 3,10, 5, 0], | |
| [15,12, 8, 2, 4, 9, 1, 7, 5,11, 3,14,10, 0, 6,13] | |
| ], | |
| # S2 | |
| [ | |
| [15, 1, 8,14, 6,11, 3, 4, 9, 7, 2,13,12, 0, 5,10], | |
| [ 3,13, 4, 7,15, 2, 8,14,12, 0, 1,10, 6, 9,11, 5], | |
| [ 0,14, 7,11,10, 4,13, 1, 5, 8,12, 6, 9, 3, 2,15], | |
| [13, 8,10, 1, 3,15, 4, 2,11, 6, 7,12, 0, 5,14, 9] | |
| ], | |
| # S3 | |
| [ | |
| [10, 0, 9,14, 6, 3,15, 5, 1,13,12, 7,11, 4, 2, 8], | |
| [13, 7, 0, 9, 3, 4, 6,10, 2, 8, 5,14,12,11,15, 1], | |
| [13, 6, 4, 9, 8,15, 3, 0,11, 1, 2,12, 5,10,14, 7], | |
| [ 1,10,13, 0, 6, 9, 8, 7, 4,15,14, 3,11, 5, 2,12] | |
| ], | |
| # S4 | |
| [ | |
| [ 7,13,14, 3, 0, 6, 9,10, 1, 2, 8, 5,11,12, 4,15], | |
| [13, 8,11, 5, 6,15, 0, 3, 4, 7, 2,12, 1,10,14, 9], | |
| [10, 6, 9, 0,12,11, 7,13,15, 1, 3,14, 5, 2, 8, 4], | |
| [ 3,15, 0, 6,10, 1,13, 8, 9, 4, 5,11,12, 7, 2,14] | |
| ], | |
| # S5 | |
| [ | |
| [ 2,12, 4, 1, 7,10,11, 6, 8, 5, 3,15,13, 0,14, 9], | |
| [14,11, 2,12, 4, 7,13, 1, 5, 0,15,10, 3, 9, 8, 6], | |
| [ 4, 2, 1,11,10,13, 7, 8,15, 9,12, 5, 6, 3, 0,14], | |
| [11, 8,12, 7, 1,14, 2,13, 6,15, 0, 9,10, 4, 5, 3] | |
| ], | |
| # S6 | |
| [ | |
| [12, 1,10,15, 9, 2, 6, 8, 0,13, 3, 4,14, 7, 5,11], | |
| [10,15, 4, 2, 7,12, 9, 5, 6, 1,13,14, 0,11, 3, 8], | |
| [ 9,14,15, 5, 2, 8,12, 3, 7, 0, 4,10, 1,13,11, 6], | |
| [ 4, 3, 2,12, 9, 5,15,10,11,14, 1, 7, 6, 0, 8,13] | |
| ], | |
| # S7 | |
| [ | |
| [ 4,11, 2,14,15, 0, 8,13, 3,12, 9, 7, 5,10, 6, 1], | |
| [13, 0,11, 7, 4, 9, 1,10,14, 3, 5,12, 2,15, 8, 6], | |
| [ 1, 4,11,13,12, 3, 7,14,10,15, 6, 8, 0, 5, 9, 2], | |
| [ 6,11,13, 8, 1, 4,10, 7, 9, 5, 0,15,14, 2, 3,12] | |
| ], | |
| # S8 | |
| [ | |
| [13, 2, 8, 4, 6,15,11, 1,10, 9, 3,14, 5, 0,12, 7], | |
| [ 1,15,13, 8,10, 3, 7, 4,12, 5, 6,11, 0,14, 9, 2], | |
| [ 7,11, 4, 1, 9,12,14, 2, 0, 6,10,13,15, 3, 5, 8], | |
| [ 2, 1,14, 7, 4,10, 8,13,15,12, 9, 0, 3, 5, 6,11] | |
| ] | |
| ] | |
| def sbox_substitution(input48): | |
| """ | |
| Applies DES S-box substitution to a 48-bit input. | |
| Splits into 8 blocks of 6 bits, substitutes each using S1–S8. | |
| Parameters: | |
| input48 (int): 48-bit input after expansion and key mixing. | |
| Returns: | |
| int: 32-bit output from the 8 S-boxes | |
| """ | |
| output32 = 0 | |
| for i in range(8): | |
| # Extract 6-bit chunk | |
| six_bits = (input48 >> (42 - 6 * i)) & 0b111111 | |
| # Get row (first and last bit), column (middle 4 bits) | |
| row = ((six_bits & 0b100000) >> 4) | (six_bits & 0b000001) | |
| col = (six_bits >> 1) & 0b1111 | |
| # Get S-box value (4 bits) | |
| sbox_val = S_BOXES[i][row][col] | |
| # Append to output (shift left by 4 then OR) | |
| output32 = (output32 << 4) | sbox_val | |
| return output32 | |
| def left_rotate(val, shift, size): | |
| """Left circular shift""" | |
| return ((val << shift) & ((1 << size) - 1)) | (val >> (size - shift)) | |
| def key_schedule(key64): | |
| """ | |
| Generate 16 DES subkeys (48-bit) from the 64-bit key. | |
| Parameters: | |
| key64 (int): 64-bit integer key | |
| Returns: | |
| List[int]: 16 round keys, each 48 bits | |
| """ | |
| # Tables | |
| PC1 = [ | |
| 57,49,41,33,25,17, 9, | |
| 1,58,50,42,34,26,18, | |
| 10, 2,59,51,43,35,27, | |
| 19,11, 3,60,52,44,36, | |
| 63,55,47,39,31,23,15, | |
| 7,62,54,46,38,30,22, | |
| 14, 6,61,53,45,37,29, | |
| 21,13, 5,28,20,12, 4 | |
| ] | |
| PC2 = [ | |
| 14,17,11,24, 1, 5, | |
| 3,28,15, 6,21,10, | |
| 23,19,12, 4,26, 8, | |
| 16, 7,27,20,13, 2, | |
| 41,52,31,37,47,55, | |
| 30,40,51,45,33,48, | |
| 44,49,39,56,34,53, | |
| 46,42,50,36,29,32 | |
| ] | |
| LEFT_SHIFTS = [1, 1, 2, 2, 2, 2, 2, 2, | |
| 1, 2, 2, 2, 2, 2, 2, 1] | |
| # Step 1: Apply PC-1 | |
| key56 = permute(key64, PC1, 64) | |
| C = (key56 >> 28) & ((1 << 28) - 1) | |
| D = key56 & ((1 << 28) - 1) | |
| round_keys = [] | |
| for shift in LEFT_SHIFTS: | |
| # Step 2: Left shifts | |
| C = left_rotate(C, shift, 28) | |
| D = left_rotate(D, shift, 28) | |
| # Step 3: Combine and apply PC-2 | |
| CD = (C << 28) | D | |
| Ki = permute(CD, PC2, 56) | |
| round_keys.append(Ki) | |
| return round_keys | |
| def f_function(r32, k48): | |
| expanded = expansion_function(r32) | |
| xored = key_mixing(expanded_R=expanded, subkey=k48) | |
| substituted = sbox_substitution(xored) | |
| P_TABLE = [ | |
| 16, 7,20,21,29,12,28,17, | |
| 1,15,23,26, 5,18,31,10, | |
| 2, 8,24,14,32,27, 3, 9, | |
| 19,13,30, 6,22,11, 4,25 | |
| ] | |
| return permute(substituted, P_TABLE, 32) | |
| def encrypt(plaintext, key): | |
| """ | |
| Encrypts a 64-bit plaintext using DES. | |
| Parameters: | |
| plaintext (int): 64-bit integer plaintext | |
| key (int): 64-bit integer key | |
| Returns: | |
| int: 64-bit encrypted ciphertext | |
| """ | |
| round_keys = key_schedule(key) | |
| permuted_plaintext = initial_permutation(plaintext) | |
| left = (permuted_plaintext >> 32) & 0xffffffff | |
| right = permuted_plaintext & 0xffffffff | |
| for i in range(16): | |
| left_next = right | |
| right = left ^ f_function(right, round_keys[i]) | |
| left = left_next | |
| preoutput = (right << 32) | left | |
| return final_permutation(preoutput) | |
| key = 4860080471782942578 | |
| plain_text = 10000 | |
| cipher_text = encrypt(plaintext=plain_text, key=key) | |
| print("cipher text: ", cipher_text) | |
| print("cipher text in bin: ", bin(cipher_text)) |
The output for plaintext 1000 will be. You can play with other values, they all secret now!!!
cipher text: 17552218217441908006
cipher text in bin: 0b1111001110010110000000010111100100011110110000111101010100100110Decryption
It's only half of a store; fortunately, the decryption matches the encryption but in reverse order. Let's quickly review the decryption steps and implement them in Python code.
| def decrypt(ciphertext64, key64): | |
| """ | |
| Decrypt a 64-bit ciphertext block with DES using a 64-bit key. | |
| Arguments: | |
| ciphertext64 (int): 64-bit ciphertext | |
| key64 (int): 64-bit DES key | |
| Returns: | |
| int: 64-bit plaintext | |
| """ | |
| # Generate round keys in reverse order | |
| round_keys = key_schedule(key64)[::-1] | |
| # Initial permutation | |
| ip = permute(ciphertext64, IP, 64) | |
| L = (ip >> 32) & 0xFFFFFFFF | |
| R = ip & 0xFFFFFFFF | |
| for i in range(16): | |
| next_L = R | |
| R = L ^ f_function(R, round_keys[i]) | |
| L = next_L | |
| # Final swap and inverse permutation | |
| preoutput = (R << 32) | L | |
| return final_permutation(preoutput) |
when call back with previous example:
plain_text = decrypt(17552218217441908006, key)
print("plain_text: ", plain_text)
// output is 10000The post is so long now, let’s comment here if you have any question of DES!!!
Resources
The motivation for me to write this article is watch this series of professor Christof Paar, and read his book: Understanding Cryptography: A Textbook For Students And Practitioners (https://www.amazon.com/Understanding-Cryptography-Textbook-Students-Practitioners/dp/3642446493)
https://en.wikipedia.org/wiki/Data_Encryption_Standard



Great post!!