Introduction to Public-Key Cryptography: Some number-theoretical topics

Let's explore some math before the PK algorithm. Don't scare!!! I'm learning at you and I will try explain everything as simple as possible!!!!

Brief introduction

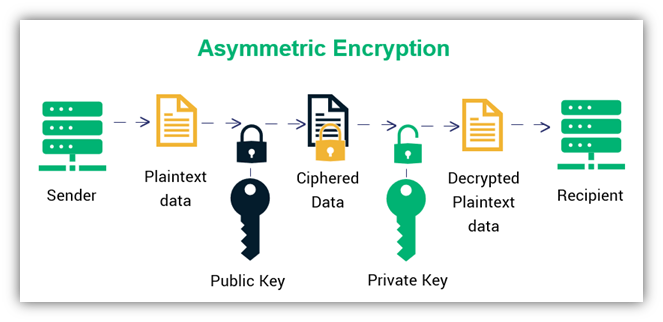
We are discussing about public-key cryptography, another alias is asymmetric cryptography. They both the same meaning.

The main difference between asymmetric and symmetric algorithms (such as DES, AES) lies in the use of keys. In asymmetric encryption, different keys are used for encryption and decryption. For example, if Alice wants to send a message to Bob, she uses Bob’s public key to encrypt it. This key is publicly available and can be accessed by anyone. When Bob receives the message, he uses his private key, which is known only to him, to decrypt it. Therefore, asymmetric encryption involves a key pair: a public key (shared with everyone) and a private key (kept secret by the owner).

To understand detail of PK algorithms, understand those number theory is very keep essential. Those topic are: Euclidean algorithm, Euler’s phi, Fermat’s Little Theorem and Euler’s Theorem.

Euclidean Algorithm (EA)

Let’s start with problem find greatest common divisor (gcd).

Greatest common divisor of two positive integers a and b is the largest positive integer that divides all of the r0 and r1 without a remainder and denote by gcd(a, b)

Example, gcd(15, 20) = 5. For small numbers, the gcd is easy to calculate by factoring both numbers and finding the highest common factor.

Example, Let a = 84 and b = 33. Find gcd(86, 33)?

• 84 = 2·2·3·7

• 30 = 2·3·5

Then gcd(84, 30) = 2·3 = 6.

For larger number, such as 123123777799 or 76493029347845938 the above method will take a lot of time.

The Euclid's algorithm

Source: https://www.scaffoldedmath.com/2018/02/euclidean-algorithm.html

1. Do an Euclid's Division on the bigger integer (A) by the lower (B), keep the rest and B

2. If the rest = 0 then gcd = B else, do the step 1 again with A = B and B = rest.

The Python code:

def gcd(a, b):
    if a == 0:
        return b
    return gcd(b%a, a)

Example, Let a = 973 and b = 301, gcd(973, 301) will be computed

1. 973 = 3·301 + 70, gcd(973, 301) = gcd(301, 70)

2. 301 = 4·70 + 21, gcd(301, 70) = gcd(70, 21)

3. 70 = 3·21 + 7, gcd(70, 21) = gcd(21, 7)

4. 21 = 3·7 + 0, gcd(21, 7) = gcd(7, 0) = 7

Then gcd(973, 301) = 7

Extended Euclidean Algorithms (EEA)

EEA computes a linear combination of the form:

\(\gcd(a, b) = s \cdot a + t \cdot b. \text{Where } s \text{ and } t \text{ are integer coefficients.} \)

The extended Euclidean algorithm works by keeping track of the intermediate remainders and division results within the Euclid's algorithm and using them to calculate the coefficients.

At each step of the algorithm, the previous remainders and division results are used to calculate the new coefficients. The algorithm continues until the final remainder is zero.

def extended_euclidean_algorithm(a, b):
    """
    Computes the greatest common divisor (GCD) of a and b,
    and finds integers x and y such that ax + by = gcd(a, b).

    Args:
        a: The first integer.
        b: The second integer.

    Returns:
        A tuple (g, x, y) where g is the GCD of a and b,
        and x and y are the coefficients satisfying Bézout's identity.
    """
    if a == 0:
        return b, 0, 1
    else:
        g, x_prev, y_prev = extended_euclidean_algorithm(b % a, a)
        x = y_prev - (b // a) * x_prev
        y = x_prev
        return g, x, y

Example:

extended_euclidean_algorithm(973, 301) = (7, 13, -42)
Verify: -13 * 973 - 42 * 301 = 7 (Correct)

But, why we need find those numbers?

The main application of the EEA is find an modular inverse of an integer. As we know,

\(a^{-1} \text{ exists in } \mathbb{Z}_m \text{ if } \gcd(a, m) = 1 \)

But we do not know what value of inverse element, we only know that the inverse element exists. With EEA, if seem clear now, by finding 2 integer s and t such as:

\( s \cdot a + t \cdot b = 1 \Rightarrow s \cdot 0 + t \cdot b \equiv 1 \pmod{a} \Rightarrow t \cdot b \equiv 1 \pmod{a} \)

This shows that t is the modular inverse of b in modular a.

Example, let’s find inverse of 12 in mod 67.

• We check that gcd(67, 12) = 1 then the inverse of 12 exists in modular 67.

• Find s and t by feed 67, 12 into EEA. extended_euclidean_algorithm(67, 12) = (1, -5, 28) => s = -5 and t = 28 => 12^-1 = 28 in mod 67.

• Verify: 12 * 28 = 336 ≡ 1 mod 67.

Euler’s Phi Function

Euler, yes, you correct!! he’s every where. List of his work: https://en.m.wikipedia.org/wiki/List_of_topics_named_after_Leonhard_Euler Source: https://www.reddit.com/r/mathmemes/comments/pm82vx/hes_everywhere

We consider have a ring Zm with m elements:

\(\mathbb{Z}_m = \{ 0, 1, 2, \ldots, m - 1 \}\)

We want to determine how many numbers in the set Zm are relatively prime to m—that is, how many elements i∈Zm satisfy gcd⁡(i, m)=1. This count is denoted by Φ(m). It might look unfamiliar at first, but it's a fundamental concept in the RSA algorithm.

Example with Z6 = {0, 1, 2, 3, 4, 5, 6}

gcd(0, 6) = 6
gcd(1, 6) = 1 *
gcd(2, 6) = 2
gcd(3, 6) = 3
gcd(4, 6) = 2
gcd(5, 6) = 1 *
There are 2 prime elements => Φ(6) = 2

Example with Z5 = {0, 1, 2, 3, 4, 5}

gcd(0, 5) = 5
gcd(1, 5) = 1 *
gcd(2, 5) = 1 *
gcd(3, 5) = 1 *
gcd(4, 5) = 1 *
=> Φ(5) = 4

Calculate by this method is very slow if we need for large numbers. Fortunately we have another algorithm to compute Φ.

If we can write m as follow

\(m = p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_n^{e_n}. \)

\(\text{ Where the \( p_i \) are distinct prime numbers and the \( e_i \) are positive integers}\)

\(\text{Then, we have: } \Phi(m) = \prod_{i=1}^{n} \left( p_i^{e_i} - p_i^{e_i - 1} \right)\)

Example with m = 240, somehow we know how to factorization of 240:

\(m = 240 = 16 \cdot 15 = 2^4 \cdot 3 \cdot 5\)

\(\text{Then: } \Phi(m) = \left(2^4 - 2^3\right) \cdot \left(3^1 - 3^0\right) \cdot \left(5^1 - 5^0\right) = 8·2·4 = 64.\)

Fermat’s Little Theorem

Don’t confuse this with Fermat’s Last Theorem in this meme.

Source: https://x.com/MathMatize/status/1834247856221294762

\(\text{Let } a \text{ be an integer and } p \text{ a prime. Then: } a^p \equiv a \pmod{p} \)

Example:

• a= 5, p = 7 => 5^7 mod 7 = 78125 mod 7 = 5 => 5^7 ≡ 5 mod 7

• a = 10, p = 7 => 10 ^ 7 mod 7 = 10 mod 7 = 3 => 10^7 ≡ 3 mod 7 ( Note: 10 ≡ 3 mod 7)

Base on Fermat’s little theorem we have:

\(a^{p-1} \equiv 1 \pmod{p} \quad \text{and} \quad a^{-1} \equiv a^{p-2} \pmod{p}\)

This provides an alternative to the EEA for computing inverse of a.

Example: p = 7 and a = 5, we can compute inverse of 5 in mod 7 equal 5^(7-2) = 5^5 ≡ 3 mod 7. Verify 5*3 = 15 ≡ 1 mod 7. => 5^-1 = 3 in mod 7.

Euler’s Theorem

\(\text{Let } a \text{ and } m \text{ be integers with } \gcd(a, m) = 1. \text{ Then: } a^{\Phi(m)} \equiv 1 \pmod{m}\)

Let’s verify with small number: Let m = 12 and a = 5,

Φ(12) = Φ(2^2*3) = (2^2 - 2^1) * (3^1 - 3^0) = 2 * 2 = 4
5^4 = 625 ≡ 1 mod 12 (correct!!)

If p is prime, then

\(\Phi(p) = p^1 - p^0 = p - 1 \Rightarrow a^{\Phi(p)} = a^{p - 1} \equiv 1 \pmod{p} \)

which is exactly Fermat's Little Theorem.

Summary

• The extended Euclidean algorithm allows us to compute modular inverses quickly, which is important for almost all public-key schemes.

• Euler’s phi function gives us the number of elements smaller than an integer n that are relatively prime to n. This is an important function for the RSA crypto- graphic scheme.

• Euler’s theorem is general for Fermat's Little Theorem.

If you have any questions, leave a comment in here!!

Resource:

• Most of resource in this post come from this book, read the book to more understand. Paar, C., Pelzl, J., Güneysu, T. (2024). Introduction to Public-Key Cryptography. In: Understanding Cryptography. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-69007-9_6

• https://www.ctfrecipes.com/cryptography/general-knowledge/maths/modular-arithmetic/greatest-common-divisor