Modular Arithmetic

In this post, we'll explore some basic arithmetic operations in finite elements. Don't worry — we'll keep it simple and easy to follow. (Spoiler: I'm not great at math either!) ➕➖✖️➗

I'll keep the theory as short as possible and focus more on examples and exercises. You can find the formal definitions in the textbooks.

Definition

All most of cryptography, symmetric or asymmetric algorithm are working in finite number of element. Let’s define some general way of dealing with arithmetic in such finite sets.

Example we have a set A:

\(A = \{0,1,2,3,4,5,6,7,8,9\}\)

We can do normal operations like ➕ and ✖️. If the result is less than 9, we keep it as is. But if it's 9 or more, we apply a simple rule: take the remainder when dividing by 9.

\(3 \times 2 = 6\)

\( 8 + 5 = 13 \equiv 4 \pmod{9} \)

We will write

\(a \equiv r \pmod{m} \quad \text{if } m \mid (a - r)\)

Example:

Verify that 42 ≡ 6 mod 9.

\(42 - 6 = 36, \text{ and } 36 \text{ is divisible by } 9, \text{ so } 42 \equiv 6\pmod{9} \text{ is true.} \)

One note that remainder is not unique, example with m = 7 and a = 15 then

• 15 ≡ 1 mod 7 since 7 | (15-1).

• 15 ≡ 8 mod 7 since 7 | (15-8).

• 15 ≡ -6 mod 7 since 7 | (15 - (-6)).

We we move to the definition of integer rings. For m is a integer, we have a integer ring Zm {0,1,2,...,m−1} and we define 2 operators in“+” and “·” in the the modular of m.

\( a + b \equiv c \pmod{m} \quad (c \in \mathbb{Z}_m) \)

\( a \cdot b \equiv d \pmod{m} \quad (d \in \mathbb{Z}_m) \)

Problems

1. Compute the following result without a calculator:

   1. 15·29 mod 13.

      15 mod 13 = 2

      29 mod 13 = 3

      Then 5*29 mod 13 = 2*3 mod 13 = 6

   2. 2·29 mod 13

      29 mod 13 = 3 => 2·29 mod 13 = 2·3 mod 13 = 6

   3. 2·3 mod 13

      2·3 mod 13 = 6

   4. −11·3 mod 13

      Find r such that 13 | ( -11 - r ) => r can be 2. Check 13 | (-11-2) <=>13 | (-13) correct.

      −11·3 mod 13 = 2 * 3 = 6.

2. Compute without a calculator:

   1. 1/5 mod 13

      The question is find a number x such as 5 * x ≡ 1 mod 13 or 5 *x mod 13 = 1

      Check small value of x:

      x = 1 => 5 * 1 = 5 mod 13 = 5

      x = 2 => 5 * 2 = 10 mod 13 = 10

      ….

      x = 8 => 5 * 8 = 40 mod 13 = 1

      So 1/5 mod 13 = 8.

   2. 1/5 mod 7

      Same answer above. Find x such as: 5 * x ≡ 1 mod 7

      Check value of x:

      x = 1 => 5 * 1 = 5 mod 7 = 5

      x = 2 => 5 * 2 = 10 mod 7 = 3

      x = 3 => 5 * 3 = 15 mod 7 = 1

      So 1/5 mod 7 = 3

   3. 3·2/5 mod 7

      <=> ((6 mod 7) * (1/5 mod 7)) mod 7

      => 6 * 3 mod 7 = 4

      => 3·2/5 mod 7 = 4

3. Compute x as far as possible without a calculator

   

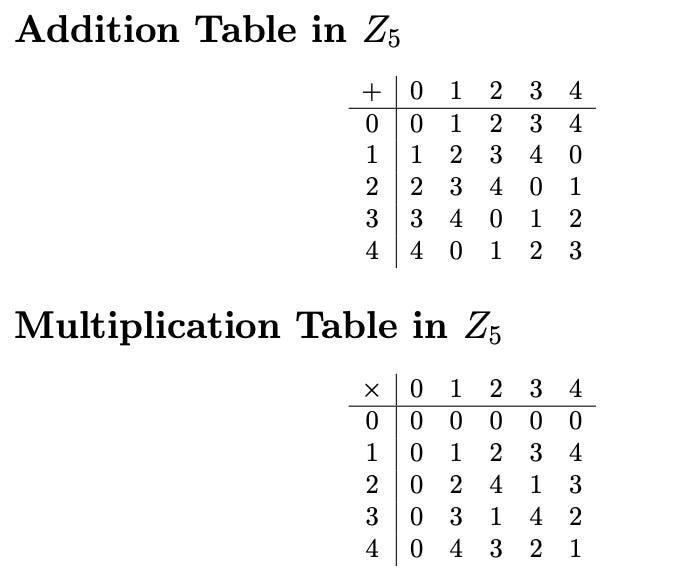
4. Construct the addition and multiplication tables for Z5

   

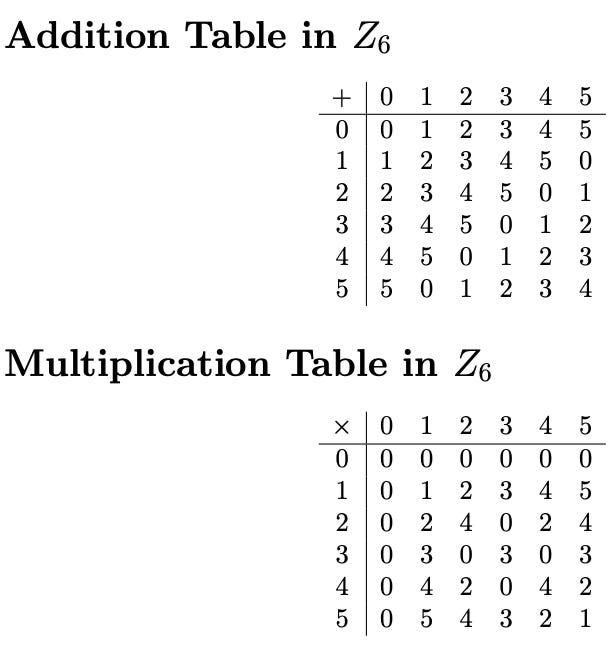
5. Construct the addition and multiplication tables for Z6.

6. 

   Note: Every nonzero element in the multiplication table of Z5​ has a multiplicative inverse, making Z5​ a field. In contrast, in Z6​, only the elements 1 and 5 have multiplicative inverses. This is related to the concepts of groups and fields, which we will discuss later.

References

• Paar, C., & Pelzl, J. (2010). Understanding Cryptography: A Textbook for Students and Practitioners. Springer.
  https://doi.org/10.1007/978-3-642-04101-3