The Advanced Encryption Standard - P2
In the previous post, we provided an overview of AES and detailed each step of the encryption process. In this post, we will focus on how to decrypt cipher text and the key schedule.
Decryption in AES
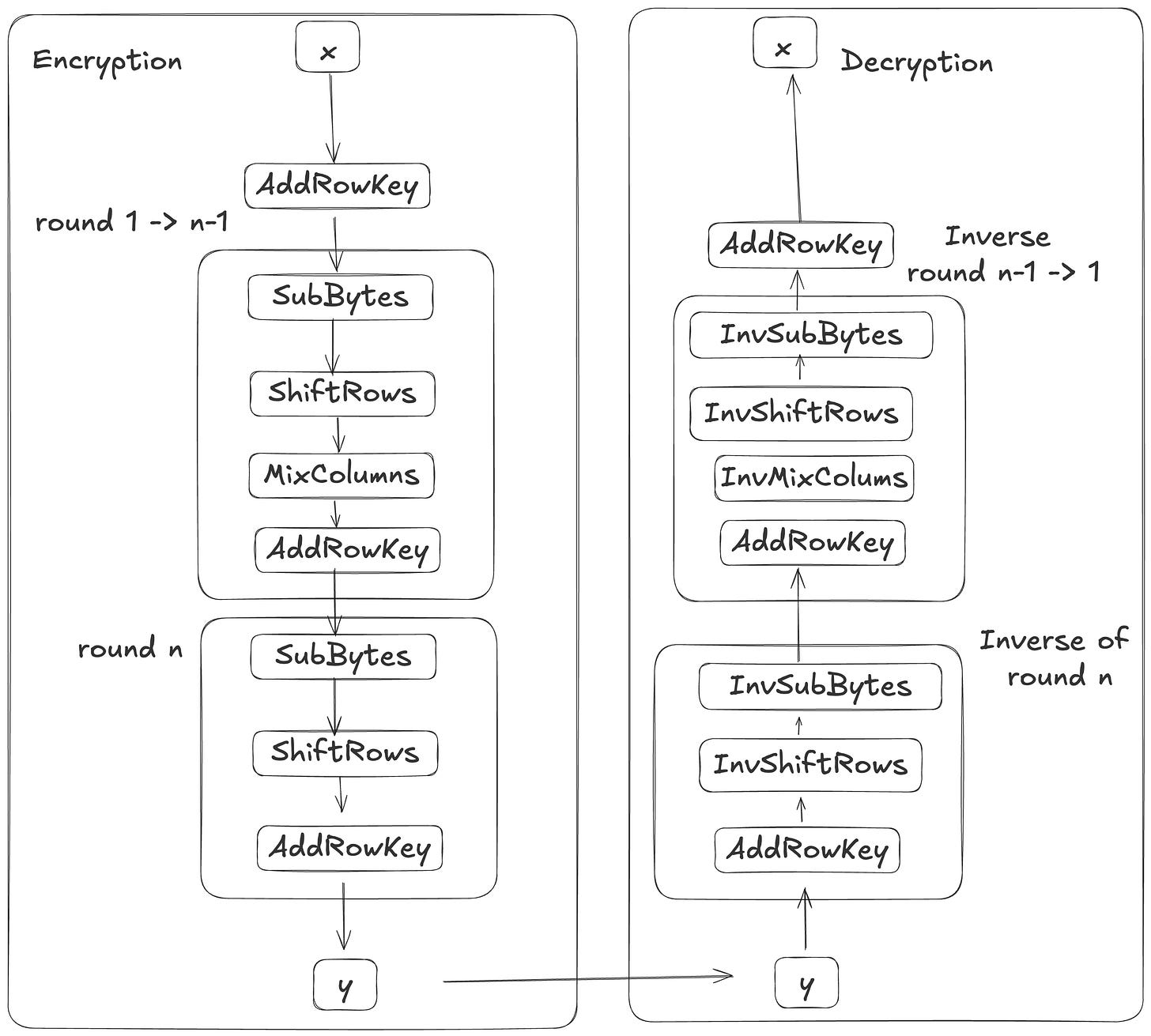
Unlike DES, which is structured as a Feistel cipher, AES does not have self-inverse steps, except for AddRoundKey step. Therefore, we need to define inverse functions for the decryption process. SubBytes becomes InvSubBytes, ShiftRows becomes InvSubRows, MixColumns becomes InvMixColumns, AddRoundKey still is AddRoundKey. Let’s revisit this diagram, but focus on right-hand side, to see the flow of decryption when Bob get the cipher text from Alice.
From the above diagram, the last row in the encryption process does not include the MixColumns step, and consequently, the first step of decryption also omits InvMixColumn. All other rounds, however, keep all steps.
InvMixColumns
Similar with MixColumns in encryption, in the InvMixColumns we have different matrix. The input is 4-byte column c multiplied by matrix 4x4. Same with MixColumn steps, those multiplication and addition in here is in finite fields GF(2^8).
Source code in Python, I re-use the mix_columns() function with different state input.
| # learned from http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c | |
| xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1) | |
| def mix_single_column(a): | |
| # see Sec 4.1.2 in The Design of Rijndael | |
| t = a[0] ^ a[1] ^ a[2] ^ a[3] | |
| u = a[0] | |
| a[0] ^= t ^ xtime(a[0] ^ a[1]) | |
| a[1] ^= t ^ xtime(a[1] ^ a[2]) | |
| a[2] ^= t ^ xtime(a[2] ^ a[3]) | |
| a[3] ^= t ^ xtime(a[3] ^ u) | |
| def mix_columns(s): | |
| for i in range(4): | |
| mix_single_column(s[i]) | |
| def inv_mix_columns(s): | |
| # see Sec 4.1.3 in The Design of Rijndael | |
| for i in range(4): | |
| u = xtime(xtime(s[i][0] ^ s[i][2])) | |
| v = xtime(xtime(s[i][1] ^ s[i][3])) | |
| s[i][0] ^= u | |
| s[i][1] ^= v | |
| s[i][2] ^= u | |
| s[i][3] ^= v | |
| mix_columns(s) |
In Python,
^= isbitwise XOR assignment operator. It performs a bitwise XOR operation between a variable and a value, and then assigns the result back to the variable. Example
a = 5 # Binary: 0101
b = 3 # Binary: 0011
a ^= b # Equivalent to a = a ^ b
print(a) # Output: 6 (Binary: 0110)InvShiftRows
In InvShiftRows, we shift each row by same position but opposite direction with ShiftRows steps.
Row # of pos shift right
----- ---------------------
1 0
2 1
3 2
4 3
| def inv_shift_rows(state): | |
| """ | |
| Perform AES Inverse ShiftRows on a 4x4 AES state (column-major format). | |
| AES inverse shifts: | |
| - Row 0: No shift | |
| - Row 1: Shift right by 1 | |
| - Row 2: Shift right by 2 | |
| - Row 3: Shift right by 3 (or left by 1) | |
| :param state: 4x4 list representing AES state (column-major) | |
| :return: new state after inverse shift | |
| """ | |
| return [ | |
| state[0], # Row 0: unchanged | |
| state[1][-1:] + state[1][:-1], # Row 1: shift right by 1 | |
| state[2][-2:] + state[2][:-2], # Row 2: shift right by 2 | |
| state[3][-3:] + state[3][:-3], # Row 3: shift right by 3 | |
| ] |
InvSubBytes
In SubBytes we use S-box to encrypt, then in InvSubByte we need construct inverse S-box based on S-box. The Inverse S-box are provide in Python code, the detail of creating those boxes are out of scope in this post.
As similar with SubByte function, we only create new inverse S-box.
| # Inverse AES S-box (256 values) | |
| inv_sbox = [ | |
| 0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, | |
| 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB, | |
| 0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, | |
| 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB, | |
| 0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, | |
| 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E, | |
| 0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, | |
| 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25, | |
| 0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, | |
| 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92, | |
| 0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, | |
| 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84, | |
| 0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, | |
| 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06, | |
| 0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, | |
| 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B, | |
| 0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, | |
| 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73, | |
| 0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, | |
| 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E, | |
| 0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, | |
| 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B, | |
| 0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, | |
| 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4, | |
| 0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, | |
| 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F, | |
| 0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, | |
| 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF, | |
| 0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, | |
| 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61, | |
| 0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, | |
| 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D | |
| ] | |
| def inv_sub_bytes(state): | |
| """ | |
| Apply Inverse SubBytes to the AES state using the inverse S-box. | |
| `state` is a 4x4 list of bytes (row x column). | |
| """ | |
| for i in range(4): | |
| for j in range(4): | |
| state[i][j] = inv_sbox[state[i][j]] |
Key schedules
Great! It done for all encrypt and decrypt steps, let’s move the the last one, the key schedule. As you've realized, in AddRowKey step, we use XOR operator to combine statue matrix with subkey matrix, how those subkeys are created from main key. This discuss in this sub section.
Key schedule in encryption
The original key (128, 192, 256 bits length) will be derives to the list of subkeys. Number of subkey equal number of round in AES + 1, due to the first AddRowKey steps. We will discuss about 128-bit key, the 192 and 256 bit keys are similar.
In AES-128, there are 10 rounds so we need 10+1=11 subkeys. The subkeys are computed recursively, it mean to get subkey ki we need to get the previous subkey ki-1 with the first k0 is the original key.
128-bit subkey are store in 4 words, then 11 subkey require 11x4=44 elements, each element is a word from W[0] … W[43]. The first 4 elements of array W is copy from original key. Then for left most element of each subkeys are computed by
Where i = 1, 2, …, 10. And g is a non-linear function with 4 bit in and 4 bit out.
Others three words of each subkey are computed by
Where i = 1, 2, …, 10 and j = 1, 2, 3.
Key schedule in decryption
The same process with key schedule in encryption but we use in revered. The last key subkey in encryption will be the first subkey in decryption. The second become the second-to-last and so on.
The source code in Python for key schedule. We re-use S-box value in previous functions.
| Rcon = [ | |
| 0x00, 0x01, 0x02, 0x04, 0x08, | |
| 0x10, 0x20, 0x40, 0x80, | |
| 0x1B, 0x36 | |
| ] | |
| def sub_word(word): | |
| return [sbox[b] for b in word] | |
| def rot_word(word): | |
| return word[1:] + word[:1] | |
| def g(word, round_index): | |
| """ | |
| g(w) = SubWord(RotWord(w)) ⊕ Rcon[round_index] applied to first byte | |
| """ | |
| word = rot_word(word) | |
| word = sub_word(word) | |
| word[0] ^= Rcon[round_index] | |
| return word | |
| def key_expansion_aes128(key): | |
| """ | |
| AES-128 Key Expansion using W_{4i} = W_{4(i - 1)} ⊕ g(W_{4i - 1}) | |
| Returns list of 44 words (each 4 bytes) | |
| """ | |
| assert len(key) == 16 | |
| W = [] # 4-byte words | |
| # Initial key: W[0] to W[3] | |
| for i in range(4): | |
| W.append(key[4*i : 4*(i+1)]) | |
| # Generate W[4] to W[43] | |
| for i in range(1, 11): # 10 rounds → i from 1 to 10 | |
| base = 4 * i | |
| prev = 4 * (i - 1) | |
| W.append([a ^ b for a, b in zip(W[prev], g(W[base - 1], i))]) # W[4i] | |
| W.append([a ^ b for a, b in zip(W[base], W[prev + 1])]) # W[4i+1] | |
| W.append([a ^ b for a, b in zip(W[base + 1], W[prev + 2])]) # W[4i+2] | |
| W.append([a ^ b for a, b in zip(W[base + 2], W[prev + 3])]) # W[4i+3] | |
| return W |
Make it together
We collect all function together and create 2 functions encrpyt_block and decrypt_block.
| # Encrypt one 16-byte block | |
| def encrypt_block(block, rk): | |
| s = [[block[r + 4*c] for c in range(4)] for r in range(4)] | |
| s = add_round_key(s, rk[0:4]) | |
| for rnd in range(1, 10): | |
| s = sub_bytes(s) | |
| s = shift_rows(s) | |
| s = mix_columns(s) | |
| s = add_round_key(s, rk[rnd*4:rnd*4+4]) | |
| s = sub_bytes(s) | |
| s = shift_rows(s) | |
| s = add_round_key(s, rk[40:44]) | |
| return [s[r][c] for c in range(4) for r in range(4)] | |
| # Decrypt one 16-byte block | |
| def decrypt_block(block, rk): | |
| s = [[block[r + 4*c] for c in range(4)] for r in range(4)] | |
| s = add_round_key(s, rk[40:44]) | |
| for rnd in range(9, 0, -1): | |
| s = inv_shift_rows(s) | |
| s = inv_sub_bytes(s) | |
| s = add_round_key(s, rk[rnd*4:rnd*4+4]) | |
| s = inv_mix_columns(s) | |
| s = inv_shift_rows(s) | |
| s = inv_sub_bytes(s) | |
| s = add_round_key(s, rk[0:4]) | |
| return [s[r][c] for c in range(4) for r in range(4)] |
Let’s run those code with the demo
# === Demo ===
key = [0x2b, 0x7e, 0x15, 0x16,
0x28, 0xae, 0xd2, 0xa6,
0xab, 0xf7, 0x15, 0x88,
0x09, 0xcf, 0x4f, 0x3c]
rk = key_expansion_aes128(key)
plaintext_str = "Encrypt me plz!!"
plaintext = list(plaintext_str.encode("utf-8")) # convert to list of bytes
cipher = encrypt_block(plaintext, rk)
plain = decrypt_block(cipher, rk)
print("Plaintext :", bytes(plaintext).decode("utf-8"))
print("Encrypted :", bytes(cipher).hex())
print("Decrypted :", bytes(plain).decode("utf-8"))The output is:
Plaintext : Encrypt me plz!!
Encrypted : 7535e9cfa137e1aec8adae25b727040f
Decrypted : Encrypt me plz!!Wrap up
We’ve just taken a deep dive into how AES works—from key expansion and encryption to decryption! 🔐 Whether you're securing cat memes or critical banking data, AES has your back.
Stay curious and keep learning! Add a comment if you have any question
Don’t forget to subscribe so you never miss a post. 🚀


greatttt