Introduction to Public-Key Cryptography: The RSA cryptosystem

The Cipher That Keeps Hackers Awake at Night

Introduction

The RSA cryptosystem is a widely used method for securing digital communication, created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman. It uses two keys: a public key to encrypt messages and a private key to decrypt them. The security of RSA relies on the difficulty of factoring large prime numbers, making it hard for attackers to break. Today, RSA is used in many areas like online banking, secure emails, and digital signatures

Public and private keys generator

Different with symmetric cryptosystem, generate keys in asymmetric require a lot of computational resource. From previous post we know that keys in PK is are pair of public and private key. This is a process to generate a pair key in RSA algorithm:

1. Choose two large primes p and q.

2. Compute n = p·q.

3. Compute Φ(n) = (p−1)(q−1).

4. Select the public exponent e ∈ {1,2,...,Φ(n)−1} such that:

\(\gcd(e, \Phi(n)) = 1\)

5. Compute the private key d such that
   

\(d \cdot e \equiv 1 \pmod{\Phi(n)}\)

Public key: kpub = (n,e) and private key: kpr = (d)

The condition in step 4 to make sure we alway find an inverse of e in module of Φ(n). the value of e and d can be compute by using EEA algorithm (https://cryptography101.substack.com/i/167888703/extended-euclidean-algorithms-eea)

Encrypt and decrypt

Let’s see how to use those keys to encrypt and decrypt in RSA:

RSA Encryption Given the public key (n,e) = kpub and the plaintext x, the encryption function is:

\(y = e_{k_{\text{pub}}}(x) \equiv x^e \pmod{n}, \quad \text{where } x, y \in \mathbb{Z}_n\)

RSA Decryption Given the private key d = kpr and the ciphertext y, the decryption function is:

\(x = d_{k_{\text{pr}}}(y) \equiv y^d \pmod{n}, \quad \text{where } x, y \in \mathbb{Z}_n\)

This is sequence diagram for the described RSA communication between Alice and Bob.

First Bob compute this public and private key and send the public key to Alice

n = 3 * 11 = 33
Φ(n) = 2 * 10 = 20
Choose e = 7. Check gcd(7, 20) = 1 => e = 7 is correct private key
d ≡ e^-1  ≡ 3 mod 20. Check 3 * 7 = 21 ≡ 1 mod 20
Bob's public key: (33, 7)
Bob's private key(3)

Then, Alice want to send to Bob a message x = 8. She get Bob’s public key (33,7) and compute:

y = 8^7 ≡ 2 mod 33. She send y = 2 to Bob

Finally, he get the message y = 2 then with this private key (d=3), he decrypt:

x = 2^3 = 8 mod 33. 

This is toy sample to show how it work, in the real project, p, q, n, e, d is very large number, example in decimal for RSA with 1024 bit.

p = 12684770141574440689879004793006036272461837910633429242399109021998171200899373570168220722670567844207428416498266325962760070525921677616815394009176451

q = 13119275115844056352327294972290650308209812578855202067999906597321694605161266721839060743331752505498510475561131134931460742876635574272289160444512811

Public key (n, e): (166414989268559247478580567378989328773799988662395600813661092650659535587172422797774665316803328909371212798000977275326994203979936528920891492771148512820508570099182621188004247124020616151081189466363649236634586753681293369178555325707510025972266424074975738587932928766360182781953793662744029013761, 65537)

Private key (d): 2252740151559528394465427570579367881407798494616099259784849261179335611767700704824639881495298126210087344359570934577835396157349289061766395105108115508259034879531891239349815007214497334475206412615441759699726270783933347939202729358941850501495726817518789448023972819135108186052886761074515437723

Fast Exponentiation

RSA is very computation intensive algorithm, for encryption we need compute y ≡ x^e mod n and in decryption: x ≡ y^d mod n with very long number. Example with x^8 we have 2 methods of calculate:

A naive method:

x^1 * x = x^2  
x^2 * x = x^3  
x^3 * x = x^4  
...  
x^25 * x = x^26  
==> Total multiplications: 26

Exponentiation by Squaring:

SQ : x     * x    = x^2
MUL: x^2   * x    = x^3
SQ : x^3   * x^3  = x^6
SQ : x^6   * x^6  = x^12
MUL: x^6   * x    = x^13
SQ : x^13  * x^13 = x^26

==> Total multiplications: 6

The approach Exponentiation by Squaring takes a total of six operations, it faster then the first approach. We will try implement in Python

def modular_pow(x, n, m):
    result = 1
    base = x % m  # Reduce base modulo m

    while n > 0:
        if n % 2 == 1:
            result = (result * base) % m  # Multiply when bit is 1
        base = (base * base) % m          # Square base each iteration
        n //= 2                           # Move to next bit
    
    return result

## Test:
print(modular_pow(2, 26, 1000))   # Output: 864
print(pow(2, 26, 1000))           # Same result using built-in

Compare with normal compute of 2^26 mod 1000

• Compute 2^26 = 67,108,864

• Take 67,108,864 mod 1000 = 864

Padding

In practice, to make RSA more probabilistic we usually padding bits into plaintext. One popular padding techniques is Optimal Asymmetric Encryption Padding (OAEP) we will explain how it work as follow

Ref: Buchanan, William J (2022). RSA Optimal Asymmetric Encryption Padding (OAEP) using Node.js. Asecuritysite.com. https://asecuritysite.com/node/node_rsa

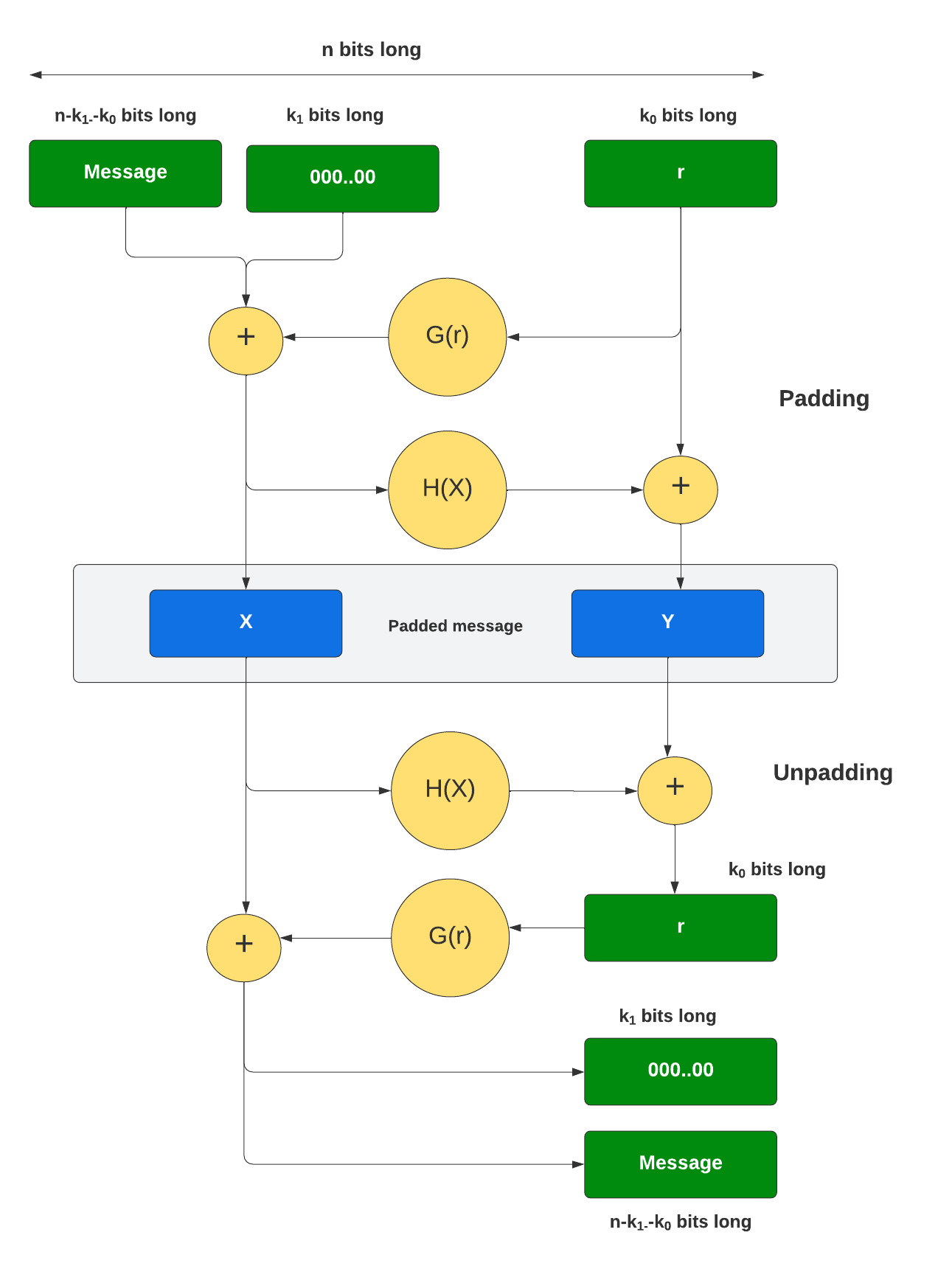
Detail as follow:

RSA Encryption with OAEP

Given a message m and the public key kpub = (n,e), the encryption function is:

\(y = e_{k_{pub}}(m) \equiv (x \,\|\, \text{pad})^e \mod n \\\)

\(\begin{align*} \text{Where: } \\ x &= (m \,\|\, 00\ldots0) \oplus H_1(\text{rand}) \\ \text{pad} &= \text{rand} \oplus H_2(x) \end{align*}\)

RSA Decryption with OAEP

Given the private key kpr = d and the ciphertext y, the decryption process is:

1. RSA decryption: dkpr (y) = yd ≡ x||pad mod n
2. recomputerand=H2(x)⊕pad
3. recompute m||00...0 = x⊕H1(rand)
4. verify that the zero string from Step 3 in fact contains z zero bits

How to find Large Primes?

The first step in key generator is find 2 large prime number p and q. If the RSA with with a 1024-bit modulus, then p and q should at have bit length 512 bits. The general approach is generate a random number and check it is prime or not. The Generate Random number should be non-predictable so if attackers can guest then the RSA easy broken.

This leads to an important problem: How quickly can we check if a number is prime? If it takes too long, then the RSA algorithm becomes impractical.

There are two popular algorithms commonly used for primality testing: Fermat's Primality Test and the Miller–Rabin Primality Test. We won’t go into the details of these algorithms here — they deserve a full post of their own, which we’ll cover later in another post.

Summary:

• RSA cryptography relies on the difficulty of factoring large numbers into their prime factors.

• RSA is very computation intensive algorithm, need use effective way to calucation.

• Padding is used to make RSA more secure.

If you have any question, just leave a comment in here, I will very happy to answer