The Advanced Encryption Standard - P1
This algorithm is one of the most widely used tools for keeping data safe—it powers things like Wi-Fi encryption and the TLS protocol. In this post, let’s dive in and explore how it works!!!
To make it easier to read, I will divide this topic into two posts. The first post will provide an overview of AES and the encryption process, while the second post will cover decryption and full source code with demo.
Overview
As mentioned in the previous article, DES with a 56-bit key is no longer secure due to advancements in computational resources. In 1997, the National Institute of Standards and Technology (NIST), part of the U.S. government, make a call for proposals for a new algorithm to replace DES. After several rounds of evaluation, Rijndael was chosen as the Advanced Encryption Standard (AES) in 2000.
AES take input plaintext in 128-bit. It supports three keys length: 128-bit, 192-bit, 256-bit. Then the output is ciphertext with length is 128 bits. Number of rounds in AES depend on the keys length.
+------------+------------+
| Key length | # of round |
+------------+------------+
| 128 bits | 10 |
| 192 bits | 12 |
| 256 bits | 14 |
+------------+------------+In DES, each round only encrypt 1/2 part of state, so it need to 16 rounds to keep secure. But in AES, each round, all of data are encrypt so number of round reduced.
In this article, we will talk about standard AES with key length is 128, named AES-128. The version of 192 and 256 is quite similar.
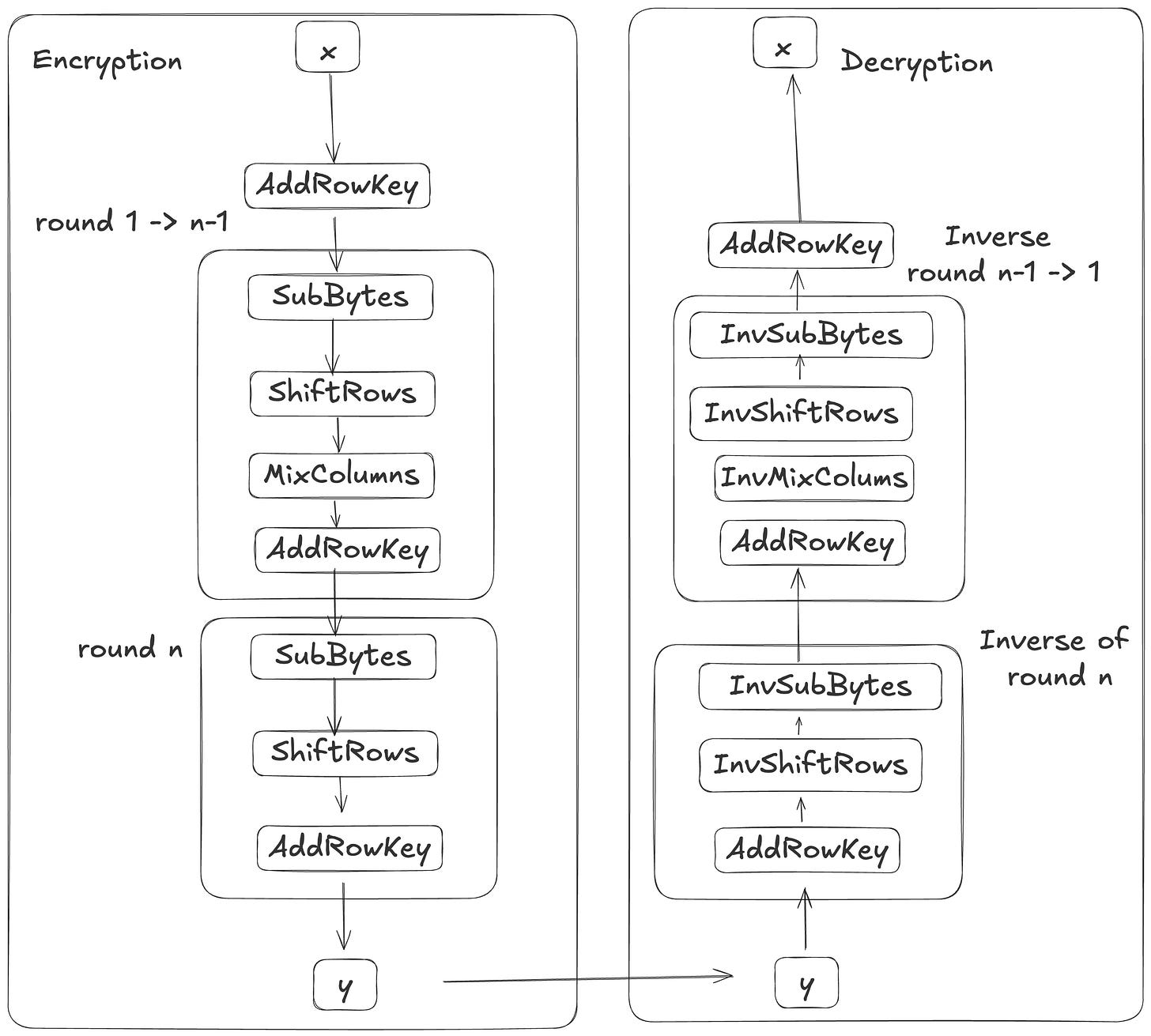
This is show AES block diagram, don’t worry if you don’t understand each block do, we will go to detail in next section include Python code to more understand.
In AES, the first step is the Key Addition layer, referred to as AddRowKey, followed by processing through n rows. Each round, except for the last one, consists of four steps: Byte Substitution (SubByte), ShiftRow, MixColumn, and AddRowKey. The last round omits the MixColumn step. Since AES is not a Feistel network, decryption requires the inverse of each step, except for AddRowKey, which is an XOR operation that is inherently reversible.
Encryption
AddRowKey
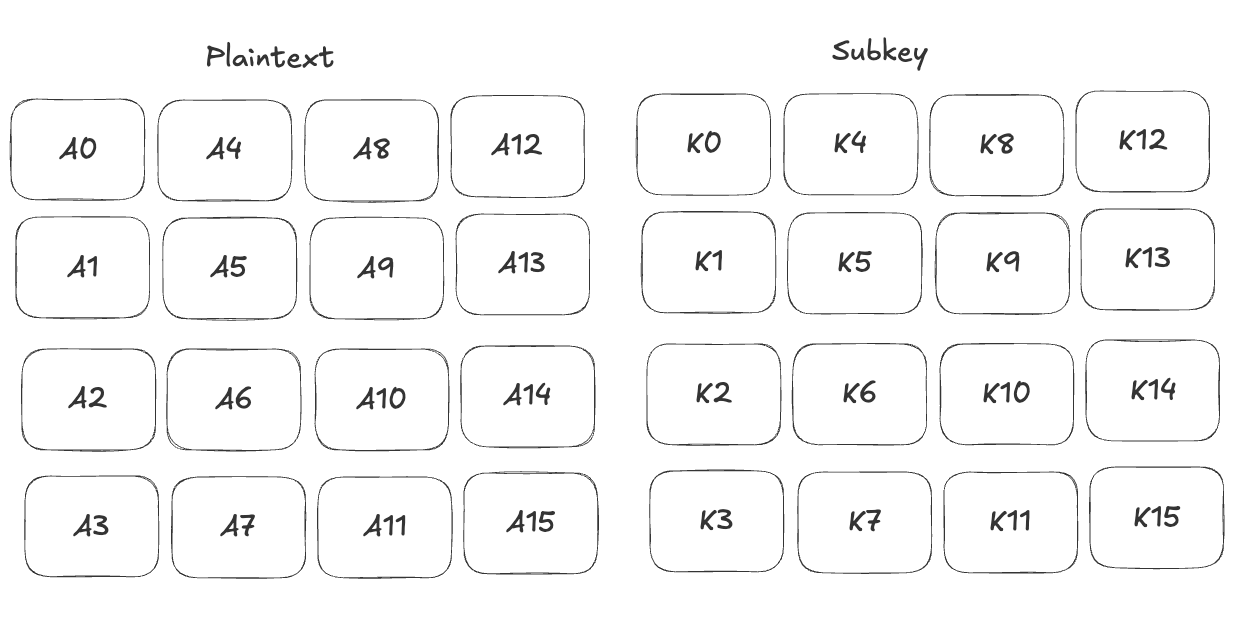
This is very simple step, a 128-bit round key, subkey, get from key schedule, XOR with the state. The state at the beginning is simply the plaintext.
Plaintext and subkey in format of 16-byte of 4-4 matrix. The AES work with byte-level, compare with DES working in bit-level. In this picture, each cell is 1 byte (8 bits) of plaintext or subkey.
The Python code is just call XOR bitwise operation each bit in 2 matrices.
| def add_round_key(state, round_key): | |
| """ | |
| XORs each byte of the state with the corresponding byte from the round key. | |
| :param state: 4x4 matrix (list of lists) representing the AES state | |
| :param round_key: 4x4 matrix (list of lists) representing the round key | |
| :return: new 4x4 matrix after XOR with round key | |
| """ | |
| return [[state[row][col] ^ round_key[row][col] for col in range(4)] for row in range(4)] |
SubByte
We can view SubByte step as a box (S-box) with 8 bits in and 8 bit out. Then we have 16 S-box, each of them are identical, it mean they are the same, make it unlike with DES where 8 different S-box are used. We each state A_i will be replace with B_i
One more mention here at S-box in nonlinear, it mean:
Detail of AES S-box in hexadecimal notion, can see in the Python code. Example we have input is (C2) hex then lookup in row C and column 2, we see the value 25. So:
Note they are in hexadecimal notation, not decimal. Then we can implement in Python by setup a predefine S-box then lookup in the input of 4-4 matrix
| # AES S-box (16x16 = 256 elements) | |
| S_BOX = [ | |
| # 0 1 2 3 4 5 6 7 8 9 A B C D E F | |
| 0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76, # 0 | |
| 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, # 1 | |
| 0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15, # 2 | |
| 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, # 3 | |
| 0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84, # 4 | |
| 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, # 5 | |
| 0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8, # 6 | |
| 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, # 7 | |
| 0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73, # 8 | |
| 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, # 9 | |
| 0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79, # A | |
| 0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08, # B | |
| 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, # C | |
| 0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e, # D | |
| 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, # E | |
| 0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 # F | |
| ] | |
| def sub_bytes(state): | |
| """ | |
| Apply the SubBytes step using the AES S-box to each byte in the state. | |
| :param state: 4x4 matrix of bytes | |
| :return: new state with each byte substituted via S-box | |
| """ | |
| return [[S_BOX[byte] for byte in row] for row in state] |
ShiftRow
After move the the SubByte steps, next step is ShiftRow, in this transformation, each row of state matrix is shift to the right by x position. Where
Row # of pos shift left
----- ---------------------
1 0
2 3
3 2
4 1
+----+----+-----+-----+ +-----+-----+-----+-----+
| B0 | B4 | B8 | B12 | | B0 | B4 | B8 | B12 | un-change
+----+----+-----+-----+ +-----+-----+-----+-----+
| B1 | B5 | B9 | B13 | | B5 | B9 | B13 | B1 | 3 pos shift left
+----+----+-----+-----+ => +-----+-----+-----+-----+
| B2 | B6 | B10 | B14 | | B10 | B14 | B2 | B6 | 2 pos shift left
+----+----+-----+-----+ +-----+-----+-----+-----+
| B3 | B7 | B11 | B15 | | B15 | B3 | B7 | B11 | 1 pos shift left
+----+----+-----+-----+ +-----+-----+-----+-----+| def shift_rows(state): | |
| """ | |
| Perform AES ShiftRows on a 4x4 AES state (column-major format). | |
| The state is a list of 4 rows, each containing 4 bytes (state[row][col]). | |
| AES shifts: | |
| - Row 0: No shift | |
| - Row 1: Shift left by 1 | |
| - Row 2: Shift left by 2 | |
| - Row 3: Shift left by 3 (or right by 1) | |
| :param state: 4x4 list representing AES state (column-major) | |
| :return: shifted 4x4 state (new list) | |
| """ | |
| return [ | |
| state[0], # Row 0: unchanged | |
| state[1][1:] + state[1][:1], # Row 1: shift left by 1 | |
| state[2][2:] + state[2][:2], # Row 2: shift left by 2 | |
| state[3][3:] + state[3][:3], # Row 3: shift left by 3 | |
| ] |
MixColumn
In MixColumn steps, 4 bytes of each column state are multiplication with a fixed, predefine matrix. With the ShiftRow and MixColumn, they make AES more diffusion. The MixColumn function take 16 byte in and 16 byte out.
More detail, example in the first column.
Let’s dive into the multiplication between the matrix and the vector shown above. Each element c_i and b_i is an 8-bit value, representing an element in a Galois field. We’ll cover Galois fields in more detail in a future post. As for the matrix, its values are written in hexadecimal, which correspond to the following binary equivalents:
01 = 0000 0001
02 = 0000 0010
03 = 0000 0011 For addition, it simple is XOR bitwise. For the multiplication, it quite complex, each single byte of each column therefore affects all the bytes of the resulting column. The implementation details are nuanced; this page and Wikipedia do a good job of covering them. Read more to understand them.
| # learned from http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c | |
| xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1) | |
| def mix_single_column(a): | |
| # see Sec 4.1.2 in The Design of Rijndael | |
| t = a[0] ^ a[1] ^ a[2] ^ a[3] | |
| u = a[0] | |
| a[0] ^= t ^ xtime(a[0] ^ a[1]) | |
| a[1] ^= t ^ xtime(a[1] ^ a[2]) | |
| a[2] ^= t ^ xtime(a[2] ^ a[3]) | |
| a[3] ^= t ^ xtime(a[3] ^ u) | |
| def mix_columns(s): | |
| for i in range(4): | |
| mix_single_column(s[i]) |
That wraps up the encryption section. We'll explore the decryption process in the next post. See you there—and don't forget to subscribe so you’ll get notified when it’s published. Happy learning! 🎉
Any issue or need discuss more,


Love this post!!!!